Zadanie nr 1047582
Dany jest rosnący ciąg geometryczny 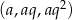 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 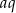 tego ciągu.
tego ciągu.
Rozwiązanie
Wiemy, że ciąg 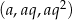 jest rosnący, więc jego największym wyrazem jest
jest rosnący, więc jego największym wyrazem jest 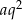 . W takim razie ciąg
. W takim razie ciąg 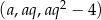 jest arytmetyczny i mamy
jest arytmetyczny i mamy
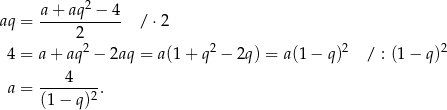
Z założenia  i
i 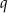 są liczbami całkowitymi, więc
są liczbami całkowitymi, więc 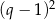 jest kwadratem liczby całkowitej dzielącym 4. Zatem
jest kwadratem liczby całkowitej dzielącym 4. Zatem 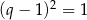 lub
lub 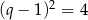 . Pierwsza możliwość odpada, bo z założenia
. Pierwsza możliwość odpada, bo z założenia 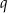 jest liczbą nieparzystą. Zatem
jest liczbą nieparzystą. Zatem 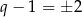 , czyli
, czyli 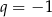 lub
lub 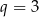 . Tylko w drugim przypadku otrzymujemy ciąg rosnący, więc
. Tylko w drugim przypadku otrzymujemy ciąg rosnący, więc 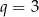 i
i
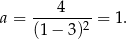
Stąd 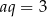 .
.
Odpowiedź: