/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 1533993

Dodaj do ulubionych
Dodaj do rozwiązanych

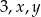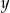Liczby 3,x,y są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę x zmniejszymy o 5, a liczbę y zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe x i y .

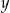Rozwiązanie

Sposób I

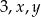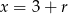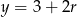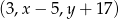Wiemy, że liczby 3,x,y są kolejnymi wyrazami ciągu arytmetycznego, więc x = 3 + r i y = 3 + 2r dla pewnego r . Wiemy ponadto, że ciąg (3,x − 5 ,y + 1 7) jest ciągiem geometrycznym, więc

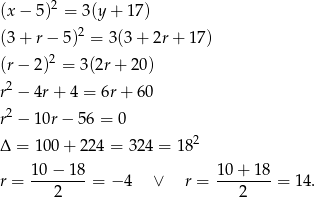
2 (x − 5 ) = 3(y+ 17) (3 + r − 5)2 = 3(3 + 2r + 17) (r − 2)2 = 3(2r + 20 ) 2 r − 4r + 4 = 6r + 60 r2 − 10r − 56 = 0 2 Δ = 100 + 22 4 = 324 = 18 10− 18 10 + 18 r = --------= − 4 ∨ r = --------= 14. 2 2

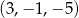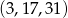Otrzymujemy stąd dwa ciągi: (3,− 1,− 5) i (3,1 7,31) .

Sposób II

Wiemy, że ciąg 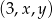(3 ,x,y) jest arytmetyczny, więc

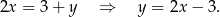
2x = 3 + y ⇒ y = 2x − 3.

Wiemy ponadto, że ciąg 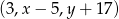(3,x − 5,y + 17) jest geometryczny, więc

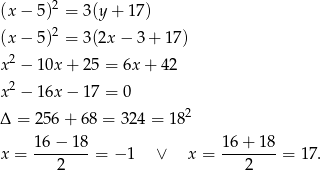
(x − 5)2 = 3(y + 1 7) 2 (x − 5) = 3(2x − 3+ 17) x2 − 10x + 2 5 = 6x + 42 x2 − 16x − 1 7 = 0 2 Δ = 256 + 68 = 3 24 = 18 16−--18- 16-+-1-8 x = 2 = − 1 ∨ x = 2 = 17.

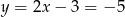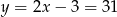Mamy wtedy odpowiednio y = 2x − 3 = − 5 i y = 2x − 3 = 31 .  
Odpowiedź: 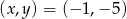(x,y ) = (− 1,− 5) lub (x,y ) = (17,31)

Wersja PDF