Zadanie nr 2048221
Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi oraz siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.
Rozwiązanie
Z podanej informacji o sumie i o ciągu geometrycznym mamy układ równań.
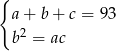
Dodatkowo mamy informację o ciągu arytmetycznym, z której otrzymujemy 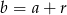 i
i 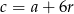 . Mamy więc równania
. Mamy więc równania
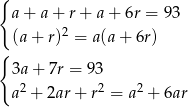
Przekształćmy drugie równanie
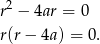
Jeżeli 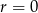 to mamy
to mamy 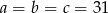 . Jeżeli natomiast
. Jeżeli natomiast 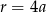 to z pierwszego równania mamy
to z pierwszego równania mamy
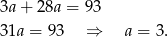
Wtedy 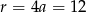 ,
, 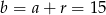 i
i 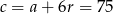 .
.
Odpowiedź: 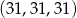 lub
lub