Zadanie nr 2121162
Trzy liczby tworzą rosnący ciąg geometryczny. Suma tych liczb jest równa 28. Liczby te są jednocześnie 1, 2 i 4 wyrazem ciągu arytmetycznego. Jakie to liczby?
Rozwiązanie
Z podanej informacji o sumie i o ciągu geometrycznym mamy układ równań.
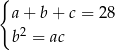
Dodatkowo mamy informację o ciągu arytmetycznym, z której otrzymujemy 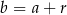 i
i 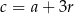 . Mamy więc równania
. Mamy więc równania
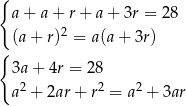
Przekształćmy drugie równanie
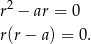
Jeżeli 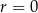 to
to 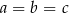 , co jest sprzeczne z założeniem, że ciąg ma być rosnący. Zatem
, co jest sprzeczne z założeniem, że ciąg ma być rosnący. Zatem 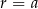 i z pierwszego równania mamy
i z pierwszego równania mamy
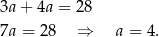
Wtedy 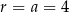 ,
, 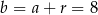 i
i 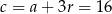 .
.
Odpowiedź: