Zadanie nr 2332285
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Rozwiązanie
Sposób I
Wiemy, że szukane liczby są kolejnymi wyrazami ciągu arytmetycznego, czyli są postaci: 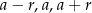 . W dodatku znamy ich sumę
. W dodatku znamy ich sumę
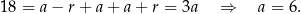
Zatem szukane liczby są postaci 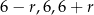 . Nie wiemy, która z tych liczb jest największa, więc musimy rozważyć dwa przypadki.
. Nie wiemy, która z tych liczb jest największa, więc musimy rozważyć dwa przypadki.
Jeżeli 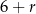 jest największą liczbą, to wiemy, że
jest największą liczbą, to wiemy, że 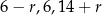 są kolejnymi wyrazami ciągu geometrycznego, czyli
są kolejnymi wyrazami ciągu geometrycznego, czyli
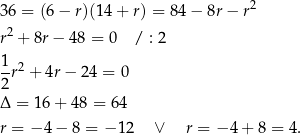
Ponieważ założyliśmy, że 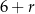 jest największą z danych liczb, więc mamy
jest największą z danych liczb, więc mamy 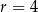 , czyli ciąg
, czyli ciąg 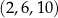 .
.
Jeżeli 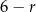 jest największą liczbą, to wiemy, że
jest największą liczbą, to wiemy, że 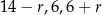 są kolejnymi wyrazami ciągu geometrycznego, czyli
są kolejnymi wyrazami ciągu geometrycznego, czyli
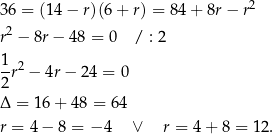
Ponieważ założyliśmy, że 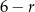 jest największą z danych liczb, więc mamy
jest największą z danych liczb, więc mamy 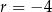 , czyli ciąg
, czyli ciąg 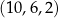 .
.
Sposób II
Szukamy trzech liczb 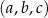 tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg
tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg 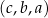 też jest arytmetyczny, możemy założyć (na użytek rachunków), że
też jest arytmetyczny, możemy założyć (na użytek rachunków), że 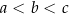 (jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby
(jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby 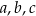 mają spełniać układ równań
mają spełniać układ równań
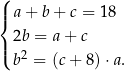
Z pierwszych dwóch równań mamy
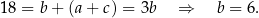
W takim razie
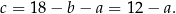
Podstawiamy uzyskane wartości do trzeciego równania i mamy
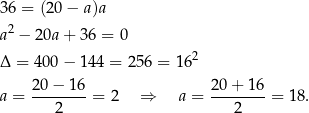
Ponieważ założyliśmy, że 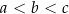 , drugie rozwiązanie odpada i mamy
, drugie rozwiązanie odpada i mamy 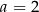 . Wtedy
. Wtedy 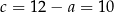 . Pomijając złożenie
. Pomijając złożenie 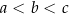 otrzymujemy drugi ciąg spełniający warunki zadania:
otrzymujemy drugi ciąg spełniający warunki zadania: 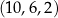 .
.
Odpowiedź: 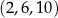 lub
lub