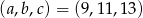/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 2830222

Dodaj do ulubionych
Dodaj do rozwiązanych

Ciąg liczbowy 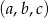(a,b,c) jest arytmetyczny i 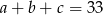a+ b+ c = 33 , natomiast ciąg 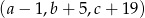(a − 1,b + 5,c + 19) jest geometryczny. Oblicz a,b ,c .

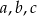Rozwiązanie

Skoro podane liczby są kolejnymi wyrazami ciągu arytmetycznego, możemy je oznaczyć przez 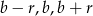b− r,b,b + r . Z podanej sumy mamy więc

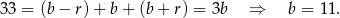
33 = (b − r)+ b+ (b+ r) = 3b ⇒ b = 1 1.

Zatem szukane liczby to 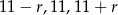11 − r,11,11 + r .

Pozostało teraz skorzystać z drugiej informacji: jeżeli trzy liczby są kolejnymi wyrazami ciągu geometrycznego, to kwadrat środkowej musi być równy iloczynowi pozostałych, czyli

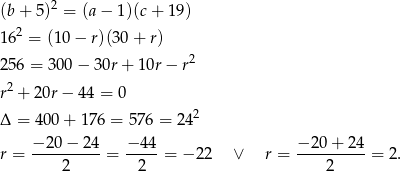
2 (b + 5 ) = (a− 1)(c+ 1 9) 162 = (10 − r)(30 + r) 2 256 = 300 − 30r + 1 0r− r r2 + 20r − 44 = 0 Δ = 40 0+ 176 = 576 = 242 − 20− 24 − 44 − 20 + 24 r = ----------= -----= − 22 ∨ r = ----------= 2. 2 2 2

Są zatem dwa takie ciągi

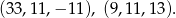
(33,11,− 11), (9,11,13 ).

 
Odpowiedź: 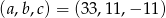(a,b,c) = (3 3,11,− 11) lub (a,b,c) = (9 ,11,13)

Wersja PDF