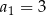/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 3655778

Dodaj do ulubionych
Dodaj do rozwiązanych

W trzywyrazowym ciągu geometrycznym 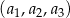(a1,a2,a3) spełniona jest równość 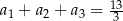a1 + a2 + a3 = 133 . Wyrazy 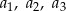a1, a2, a3 są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz a 1 .

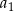Rozwiązanie

Z podanej informacji o sumie i o ciągu geometrycznym mamy układ równań.

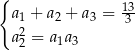
{ a1 + a2 + a3 = 133 a2 = a a 2 1 3

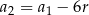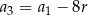Dodatkowo mamy informację o ciągu arytmetycznym, z której otrzymujemy a2 = a 1 − 6r i a3 = a1 − 8r . Mamy więc równania

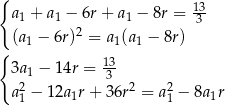
{ 13 a1 + a1 − 6r+ a1 − 8r = -3 (a1 − 6r)2 = a1(a1 − 8r) { 3a1 − 14r = 13 2 3 2 2 a1 − 12a1r + 36r = a 1 − 8a 1r

Przekształćmy drugie równanie

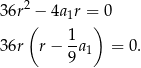
2 36r − 4a 1r = 0 ( 1 ) 36r r− -a1 = 0. 9

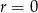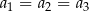Jeżeli r = 0 , to a1 = a2 = a3 , co jest sprzeczne z założeniem, że ciąg arytmetyczny ma być rosnący. Zatem 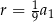r = 19a1 i z pierwszego równania mamy

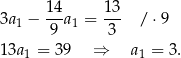
14 13 3a1 − --a1 = --- /⋅ 9 9 3 13a1 = 39 ⇒ a 1 = 3.

 
Odpowiedź: a1 = 3

Wersja PDF