/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 4061592

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzywyrazowy ciąg 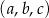(a,b,c) o wyrazach dodatnich jest arytmetyczny, natomiast ciąg

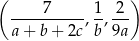
( ) ----7-----, 1-, 2 a+ b+ 2c b 9a

jest geometryczny. Oblicz iloraz ciągu geometrycznego.

Rozwiązanie

Sposób I

Wiemy, że ciąg 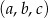(a ,b,c) jest arytmetyczny, więc 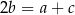2b = a+ c . Ponadto ciąg

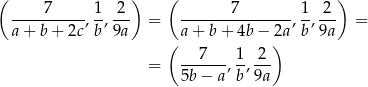
( ) ( ) -----7---- 1--2- -------7--------1- 2-- a + b + 2c ,b,9a = a+ b+ 4b − 2a,b ,9a = ( ) = --7---, 1-, 2 5b− a b 9a

jest geometryczny. W ciągu geometrycznym kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich, więc

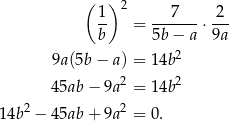
( 1) 2 7 2 -- = -------⋅--- b 5b − a 9a 9a (5b− a) = 14b2 2 2 45ab − 9a = 14b 14b2 − 45ab + 9a2 = 0.

Zanim przekształcimy to równanie dalej zauważmy, że mamy obliczyć

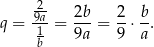
2- q = 9a-= 2b-= 2⋅ b. 1b 9a 9 a

Musimy więc obliczyć 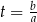t = b a . Wracamy do naszego równania.

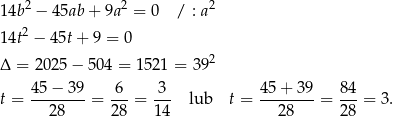
14b2 − 45ab + 9a 2 = 0 / : a 2 2 14t − 45t+ 9 = 0 Δ = 2025 − 504 = 1521 = 3 92 t = 45-−-39-= -6-= -3- lub t = 45+--39-= 84-= 3. 28 28 14 28 28

W tym miejscu łatwo popełnić błąd – zauważmy, że jeżeli 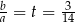ba = t = 314 , to

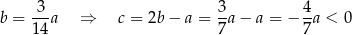
b = -3-a ⇒ c = 2b − a = 3a − a = − 4-a < 0 14 7 7

co jest sprzeczne z założeniem, że liczby: 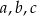a,b,c są dodatnie. Zatem 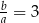ba = 3 i

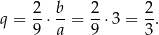
2- b- 2- 2- q = 9 ⋅ a = 9 ⋅3 = 3.

Sposób II

Jeżeli oznaczymy przez r różnicę ciągu arytmetycznego, to 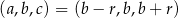(a,b,c) = (b− r,b,b+ r) i wiemy, że ciąg

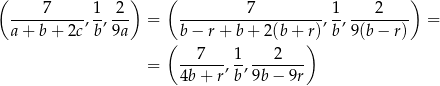
( 7 1 2 ) ( 7 1 2 ) ---------- ,-,--- = -------------------, -,-------- = a + b + 2c b 9a ( b− r+ b + 2(b + r)) b 9(b − r) --7----1- ---2---- = 4b+ r,b, 9b− 9r

jest geometryczny. W ciągu geometrycznym kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich, więc

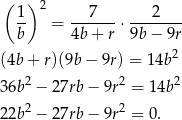
( ) 1 2 7 2 b- = 4b-+-r-⋅9b-−-9r- (4b + r)(9b − 9r) = 14b2 2 2 2 36b − 2 7rb− 9r = 14b 22b 2 − 2 7rb− 9r2 = 0.

Zanim przekształcimy to równanie dalej zauważmy, że mamy obliczyć

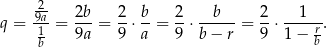
-2 2b 2 b 2 b 2 1 q = 9a1-= ---= -⋅ --= -⋅ -----= --⋅-----r. b 9a 9 a 9 b− r 9 1 − b

Interesuje nas więc iloraz 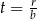t = rb . Wracamy teraz do naszego równania.

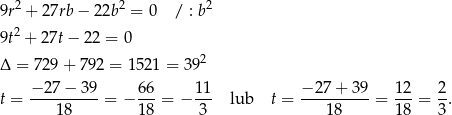
2 2 2 9r + 27rb− 22b = 0 / : b 9t2 + 27t− 2 2 = 0 2 Δ = 729+ 792 = 1 521 = 39 − 27 − 39 66 11 − 27 + 39 12 2 t = ----------= − ---= − --- lub t = ----------= ---= --. 18 18 3 18 18 3

Teraz musimy odrobinę uważać, bo wyrazy ciągu 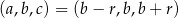(a,b,c) = (b − r,b,b+ r) mają być dodatnie, więc musi być 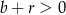b + r > 0 , czyli 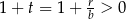1 + t = 1+ rb > 0 . Zatem pierwsze rozwiązanie odrzucamy i mamy 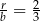-r= 2 b 3 . Stąd

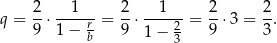
2- --1--- 2- --1--- 2- 2- q = 9 ⋅ 1− r = 9 ⋅ 1− 2 = 9 ⋅ 3 = 3. b 3

 
Odpowiedź: 2 3

Wersja PDF