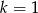Zadanie nr 4539055
- Wyznacz liczbę naturalną
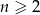 , dla której liczby
, dla której liczby 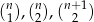 są kolejnymi wyrazami ciągu arytmetycznego;
są kolejnymi wyrazami ciągu arytmetycznego; - Dla wyznaczonej wartości
 , wyznacz liczbę naturalną
, wyznacz liczbę naturalną 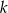 tak, aby liczby
tak, aby liczby 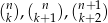 były kolejnymi wyrazami ciągu geometrycznego.
były kolejnymi wyrazami ciągu geometrycznego.
Rozwiązanie
Korzystamy z faktu, że jeżeli trzy liczby 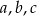 są kolejnymi wyrazami ciągu arytmetycznego to
są kolejnymi wyrazami ciągu arytmetycznego to 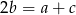 . Podobnie, jeżeli są one kolejnymi wyrazami ciągu geometrycznego, to
. Podobnie, jeżeli są one kolejnymi wyrazami ciągu geometrycznego, to 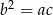 .
.
- Mamy równanie
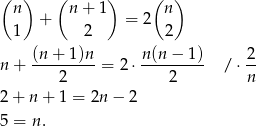
Odpowiedź: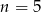
- Skoro już wiemy, że
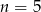 , to mamy równanie
, to mamy równanie 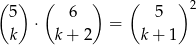
Sposób I
Ze definicji symbolu Newtona wiemy, że szukane
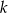 musi spełniać warunek
musi spełniać warunek 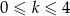 . W sumie to tylko 5 wartości, więc możemy je sprawdzić po kolei. Zanim to zrobimy, wyliczmy
. W sumie to tylko 5 wartości, więc możemy je sprawdzić po kolei. Zanim to zrobimy, wyliczmy 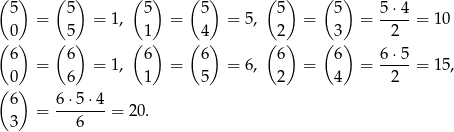
Teraz wstawiamy w naszej równości po kolei
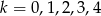 . Otrzymujemy równości
. Otrzymujemy równości 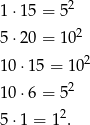
Tylko druga z tych równości jest prawdziwa, zatem
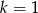 .
. Sposób II
Powyższe rachunki są znacznie prostsze jeżeli wiemy co to jest trójkąt Pascala. Rysujemy go do 6 wiersza.
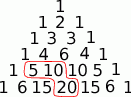
Teraz patrzymy kiedy dwie kolejne liczby w 5 wierszu i liczba po ich prawej stronie w 6 wierszu są kolejnymi wyrazami ciągu geometrycznego. Gdy to prześledzimy to jedyny taki zestaw to
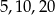 odpowiadający
odpowiadający 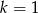 .
. Sposób III
Przekształcamy powyższe równanie
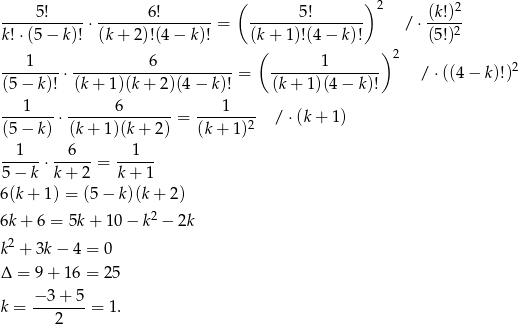
Odpowiedź: