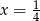/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 5775029

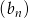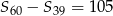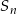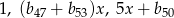Ciąg (bn) jest arytmetyczny i S60 − S39 = 10 5 , gdzie Sn oznacza sumę n początkowych wyrazów tego ciągu. Oblicz x , wiedząc, że liczby 1, (b47 + b53)x , 5x + b 50 tworzą rosnący ciąg geometryczny.

Wersja PDF

Rozwiązanie

Korzystamy ze wzoru

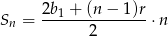
2b + (n − 1)r Sn = --1------------⋅n 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

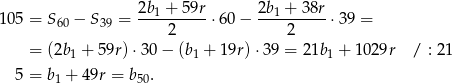
2b + 59r 2b + 38r 105 = S60 − S 39 =--1-------⋅60 − ---1------⋅39 = 2 2 = (2b 1 + 5 9r)⋅30 − (b1 + 19r) ⋅39 = 2 1b1 + 1029r / : 21 5 = b + 49r = b . 1 50

Stąd w szczególności

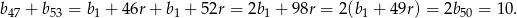
b47 + b53 = b1 + 46r + b1 + 52r = 2b 1 + 9 8r = 2(b1 + 49r) = 2b50 = 1 0.

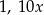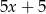Pozostało skorzystać z podanej informacji o tym, że liczby 1, 10x i 5x + 5 są kolejnymi wyrazami ciągu geometrycznego. Stąd

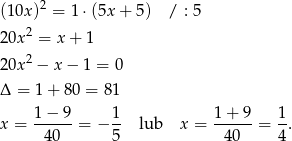
2 (10x ) = 1⋅(5x + 5) / : 5 20x 2 = x+ 1 2 20x − x − 1 = 0 Δ = 1+ 80 = 81 x = 1−--9-= − 1- lub x = 1-+-9-= 1. 40 5 40 4

Ciąg ma być rosnący, więc ujemne rozwiązanie odrzucamy i mamy 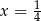1 x = 4 .  
Odpowiedź: x = 1 4

Wersja PDF