/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 6179468

Dodaj do ulubionych
Dodaj do rozwiązanych

O liczbach 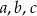a ,b ,c wiemy, że ciąg 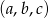(a,b,c) jest arytmetyczny i 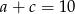a+ c = 10 , zaś ciąg 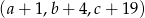(a+ 1,b+ 4,c+ 19) jest geometryczny. Wyznacz te liczby.

Rozwiązanie

Sposób I

Oznaczmy szukane liczby przez 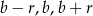b − r,b,b + r . Z warunku 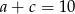a + c = 1 0 mamy

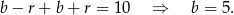
b− r+ b+ r = 10 ⇒ b = 5.

Zatem szukamy liczb postaci 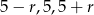5− r,5,5+ r . Pozostało teraz wykorzystać informację o tym, że liczby

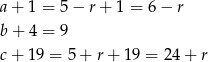
a+ 1 = 5 − r+ 1 = 6 − r b+ 4 = 9 c+ 19 = 5 + r+ 19 = 24 + r

tworzą ciąg geometryczny. Skoro tak jest, to kwadrat środkowej liczby musi być iloczynem pierwszej i trzeciej. Mamy więc równanie

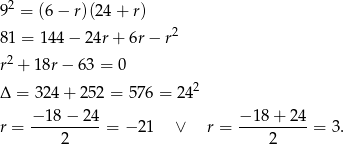
9 2 = (6− r)(24+ r) 2 8 1 = 144 − 24r + 6r − r r2 + 18r − 63 = 0 2 Δ = 324 + 2 52 = 576 = 24 − 18− 24 − 18 + 24 r = ----------= − 2 1 ∨ r = ----------= 3. 2 2

Zatem szukane liczby to 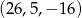(26,5,− 16) lub (2,5,8) .

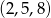Sposób II

Skoro liczby 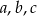a,b,c tworzą ciąg arytmetyczny to 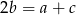2b = a+ c . Zatem

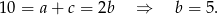
10 = a + c = 2b ⇒ b = 5.

Teraz zapiszmy informację o tym, że ciąg 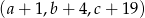(a + 1,b + 4,c + 19) jest geometryczny.

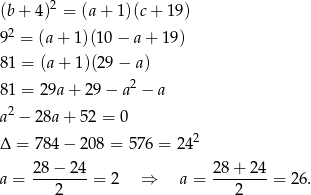
(b+ 4 )2 = (a+ 1)(c+ 19) 2 9 = (a+ 1)(10 − a+ 19) 81 = (a + 1)(29 − a) 81 = 29a + 29 − a2 − a 2 a − 2 8a+ 52 = 0 Δ = 7 84− 208 = 576 = 242 a = 28-−-24-= 2 ⇒ a = 28+--24-= 2 6. 2 2

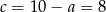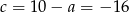Wtedy c = 10 − a = 8 i c = 10 − a = − 16 odpowiednio.  
Odpowiedź: 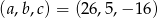(a,b,c) = (2 6,5,− 16) lub (a,b,c) = (2 ,5,8)

Wersja PDF