/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 6304580

Trzy liczby dodatnie tworzą ciąg arytmetyczny. Średnia arytmetyczna tych liczb jest równa 10. Jeśli od pierwszej odejmiemy 2, drugą pozostawimy bez zmian, a do trzeciej dodamy 7, to otrzymamy ciąg geometryczny. Wyznacz te liczby.

Wersja PDF

Rozwiązanie

Oznaczmy szukane liczby przez 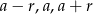a − r,a,a + r . Wtedy z podanej średniej mamy

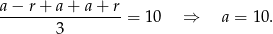
a − r + a + a+ r ----------------- = 10 ⇒ a = 10. 3

Zatem szukamy liczb postaci 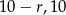10− r,10 i 10 + r .

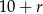Wiemy ponadto, że liczby 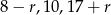8 − r,10 ,1 7+ r są kolejnymi wyrazami ciągu geometrycznego, czyli

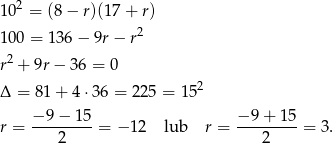
2 10 = (8− r)(1 7+ r) 2 100 = 136 − 9r − r r2 + 9r− 36 = 0 2 Δ = 81 + 4 ⋅36 = 22 5 = 15 −9 − 1 5 − 9 + 15 r = ---------= − 12 lub r = ---------= 3. 2 2

Dla 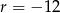r = − 12 otrzymujemy ciąg, który ma wyrazy ujemne, więc 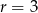r = 3 . Mamy wtedy ciąg

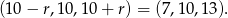
(10 − r,10,1 0+ r) = (7,10,13).

 
Odpowiedź: (7,10,1 3)

Wersja PDF