Zadanie nr 7059198
Dane są dwa różne ciągi: arytmetyczny i geometryczny. Każdy z nich składa się z trzech wyrazów dodatnich. Pierwsze i ostatnie wyrazy tych ciagów są równe. Suma wyrazów którego ciągu jest większa?
Rozwiązanie
Żeby się nie pogubić w danych, powiedzmy, że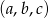 
jest ciągiem arytmetycznym, a 
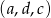ciągiem geometrycznym. Zauważmy, że z założenia są to dwa różne ciągi, więc w szczególności 
.
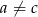Pytanie, na które musimy odpowiedzieć, to która z liczb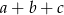 
czy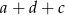 
jest większa? Oczywiście to to samo, co zapytać czy 
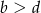, czy też na odwrót. Wiemy, że
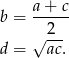
Pokażemy, że pierwsza z tych liczb jest na ogół większa (czyli, że średnia arytmetyczna jest większa od średniej geometrycznej).
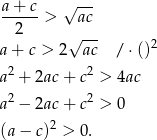
Otrzymana nierówność jest oczywiście prawdziwa. Po drodze podnosiliśmy nierówność do kwadratu, ale mogliśmy tak zrobić, bo obie strony były dodatnie.
Zatem
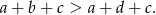
Odpowiedź: Suma ciągu arytmetycznego jest większa.
