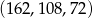/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 7439095

Pomiędzy liczby 243 i 48 wstaw takie trzy liczby, aby wraz z danymi tworzyły

  • ciąg arytmetyczny;
  • ciąg geometryczny.
Wersja PDF

Rozwiązanie

  •  

    Sposób I

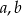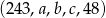    Szukamy liczb a,b i c tak aby ciąg (243,a,b,c,48) był arytmetyczny. Tak będzie jeżeli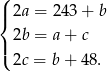

    ( |{ 2a = 243+ b 2b = a+ c |( 2c = b + 4 8.

    Podstawiamy najpierw z drugiego równania 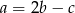a = 2b − c do pierwszego, a potem z trzeciego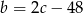 b = 2c − 48

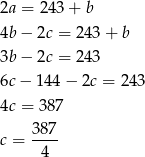
    2a = 243 + b 4b− 2c = 243 + b 3b− 2c = 243 6c− 144− 2c = 243 4c = 387 387 c = -4--

    Stąd

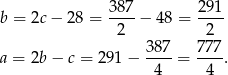
    387 291 b = 2c − 28 = ----− 48 = ---- 2 2 a = 2b − c = 2 91− 387-= 777-. 4 4

    Sposób II

    Tym razem oznaczmy szukane liczby przez 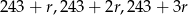24 3+ r,2 43+ 2r,243 + 3r . Przy takich oznaczeniach mamy równość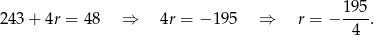

    195- 243 + 4r = 4 8 ⇒ 4r = − 195 ⇒ r = − 4 .

    To daje nam liczby

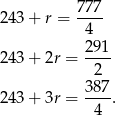
    243+ r = 777- 4 29-1 243+ 2r = 2 38 7 243+ 3r = ----. 4

     
    Odpowiedź: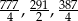 777 291 387 4 , 2 , 4

  •  

    Sposób I

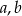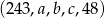    Szukamy liczby a ,b i c tak aby ciąg (243,a,b,c,48) był geometryczny. Tak będzie jeżeli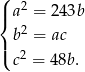

    ( |{ a2 = 243b b2 = ac |( 2 c = 48b.

    Jeżeli pomnożymy pierwsze i trzecie równanie stronami to mamy

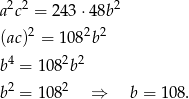
    2 2 2 a c = 243 ⋅48b (ac)2 = 1082b2 b4 = 1082b2 2 2 b = 108 ⇒ b = 108.

    Wybraliśmy dodatni pierwiastek, bo nawet jeżeli iloraz ciągu jest ujemny, to ujemne mogą być tylko a i c . Zatem

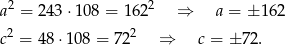
    a2 = 24 3⋅10 8 = 1622 ⇒ a = ± 162 2 2 c = 48 ⋅108 = 72 ⇒ c = ± 72.

    Jak już wcześniej zauważyliśmy, albo wszystkie liczby są dodatnie, albo ujemne są tylko a i c . Daje to nam dwa ciągi:

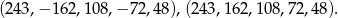
    (24 3,− 162,108,− 72,4 8),(243,162,1 08,72,48).

    Sposób II

    Tym razem oznaczmy szukane liczby przez 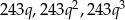2 3 2 43q,243q ,24 3q . Przy takich oznaczeniach mamy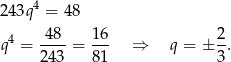

    243q4 = 4 8 q4 = -48- = 16- ⇒ q = ± 2-. 24 3 81 3

    Daje to nam dwa ciągi

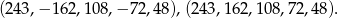
    (24 3,− 162,108,− 72,4 8),(243,162,1 08,72,48).

     
    Odpowiedź: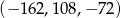 (− 162,108,− 72 ) lub (162,108 ,72)

Wersja PDF