/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 8243316

Trzy liczby, których suma jest równa 105, są kolejnymi wyrazami rosnącego ciągu geometrycznego. Pierwsza z tych liczb jest jednocześnie pierwszym, druga szóstym, a trzecia dwudziestym szóstym wyrazem pewnego ciągu arytmetycznego. Oblicz te liczby.

Wersja PDF

Rozwiązanie

Z podanej informacji o sumie i o ciągu geometrycznym mamy układ równań.

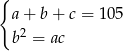
{ a + b + c = 105 b2 = ac

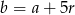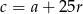Dodatkowo mamy informację o ciągu arytmetycznym, z której otrzymujemy b = a+ 5r i c = a+ 25r . Mamy więc równania

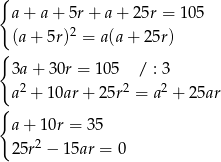
{ a+ a + 5r + a + 25r = 105 (a+ 5r )2 = a(a+ 25r) { 3a+ 30r = 105 / : 3 2 2 2 { a + 1 0ar+ 25r = a + 25ar a+ 1 0r = 35 25r2 − 15ar = 0

Z drugiego równania mamy

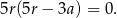
5r(5r − 3a) = 0.

Rozwiązanie 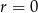r = 0 odrzucamy, bo wtedy otrzymujemy ciąg stały. W takim razie 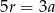5r = 3a i z pierwszego równania mamy

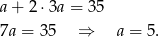
a + 2 ⋅3a = 35 7a = 3 5 ⇒ a = 5.

Stąd

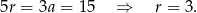
5r = 3a = 15 ⇒ r = 3.

Szukane liczby są więc równe:

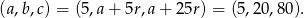
(a,b,c) = (5,a + 5r,a + 25r ) = (5,20,80).

 
Odpowiedź: (5,20,8 0)

Wersja PDF