/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 8421308

Dodaj do ulubionych
Dodaj do rozwiązanych

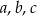Liczby a,b,c , spełniające warunek 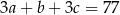3a + b + 3c = 77 , są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg 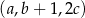(a,b + 1,2c) jest geometryczny. Wyznacz liczby 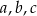a,b,c oraz podaj wyrazy ciągu geometrycznego.

Rozwiązanie

Skoro podane liczby są kolejnymi wyrazami ciągu arytmetycznego, możemy je oznaczyć przez 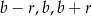b− r,b,b + r . Z podanej sumy mamy więc

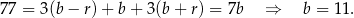
77 = 3(b − r)+ b+ 3(b+ r) = 7b ⇒ b = 11.

Zatem szukane liczby to 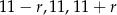11 − r,11,11 + r .

Pozostało teraz skorzystać z drugiej informacji: jeżeli trzy liczby są kolejnymi wyrazami ciągu geometrycznego, to kwadrat środkowej musi być równy iloczynowi pozostałych, czyli

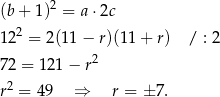
2 (b+ 1) = a ⋅2c 122 = 2(11 − r)(11 + r) / : 2 2 72 = 12 1− r r2 = 49 ⇒ r = ± 7 .

Mamy zatem

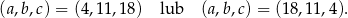
(a,b,c) = (4,11 ,1 8) lub (a,b,c) = (18,11,4).

Ciągi geometryczne to wtedy odpowiednio

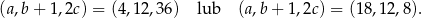
(a,b+ 1,2c) = (4,12 ,3 6) lub (a,b+ 1,2c) = (18,12,8 ).

 
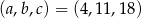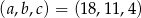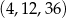Odpowiedź: (a,b,c) = (4 ,11,18) lub (a,b,c) = (1 8,11,4) , ciągi: (4,12 ,36) lub (1 8,12,8)

Wersja PDF