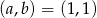/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 8524387

Dodaj do ulubionych
Dodaj do rozwiązanych

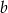Wyznacz liczby a oraz b , dla których ciąg 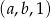(a,b ,1 ) jest ciągiem arytmetycznym, natomiast ciąg 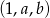(1 ,a,b) jest ciągiem geometrycznym.

Rozwiązanie

Sposób I

Jeżeli liczby 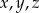x ,y,z są kolejnymi wyrazami ciągu arytmetycznego to 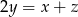2y = x+ z . Jeżeli są kolejnymi wyrazami ciągu geometrycznego to 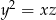y2 = xz . Mamy zatem układ równań

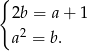
{ 2b = a + 1 2 a = b.

Podstawiając wartość 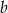b z drugiego równania do pierwszego mamy

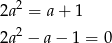
2 2a = a+ 1 2a 2 − a − 1 = 0

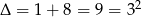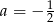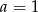Rozwiązujemy to równanie, Δ = 1+ 8 = 9 = 32 , a = − 1 2 lub a = 1 . Ponieważ 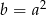2 b = a , daje to nam dwie pary rozwiązań:

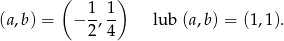
( 1 1 ) (a ,b ) = − -,-- lub (a,b ) = (1,1). 2 4

Sposób II

Jeżeli 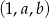(1,a,b) jest ciągiem geometrycznym to jego iloraz musi być równy 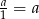a 1 = a . Zatem 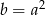2 b = a i wiemy, że ciąg 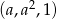2 (a,a ,1) jest ciągiem arytmetycznym. Zatem

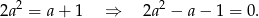
2a2 = a+ 1 ⇒ 2a2 − a− 1 = 0.

Dalej liczymy jak poprzednio.  
Odpowiedź: 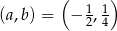( ) (a,b) = − 1, 1 2 4 lub (a,b) = (1,1)

Wersja PDF