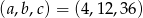/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 8674133

Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy 8, to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś do ostatniej liczby nowego ciągu arytmetycznego dodamy 64, to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby. Uwzględnij wszystkie możliwości.

Wersja PDF

Rozwiązanie

Szukamy trzech liczb 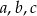a,b ,c tworzących ciąg geometryczny takich, że ciąg 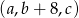(a,b + 8,c) jest arytmetyczny, a ciąg 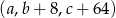(a,b + 8,c + 64) jest geometryczny.

Sposób I

Ponieważ ciąg 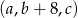(a,b + 8,c) ma być arytmetyczny to

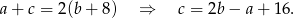
a+ c = 2(b + 8) ⇒ c = 2b − a + 16 .

Uwzględniając informacje o ciągach geometrycznych otrzymujemy układ równań.

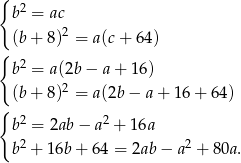
{ b2 = ac 2 { (b+ 8) = a(c + 64) b2 = a(2b − a + 16) (b+ 8)2 = a(2b − a + 16 + 64) { 2 2 b = 2ab − a + 16a b2 + 16b + 64 = 2ab − a2 + 8 0a.

Odejmujemy od drugiego równania pierwsze (żeby skrócić kwadraty) i mamy

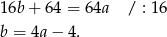
1 6b+ 64 = 64a / : 16 b = 4a− 4.

Podstawiamy to wyrażenie do pierwszego równania układu

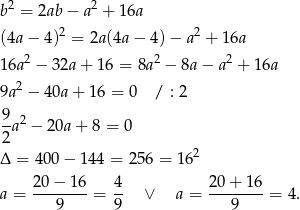
b 2 = 2ab − a2 + 16a 2 2 (4a − 4 ) = 2a(4a − 4) − a + 16a 1 6a2 − 32a+ 16 = 8a 2 − 8a − a2 + 16a 2 9a − 4 0a+ 16 = 0 / : 2 9 2 -a − 20a + 8 = 0 2 2 Δ = 40 0− 1 44 = 256 = 16 20 − 16 4 20 + 16 a = --------= -- ∨ a = --------= 4. 9 9 9

Mamy wtedy odpowiednio

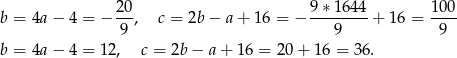
20- 9-∗16-44 100- b = 4a − 4 = − 9 , c = 2b − a + 1 6 = − 9 + 16 = 9 b = 4a − 4 = 1 2, c = 2b − a + 16 = 2 0+ 16 = 36.

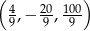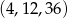Są zatem dwa ciągi spełniające warunki zadania: ( ) 4,− 20, 100 9 9 9 oraz (4,12 ,36) .

Sposób II

Dokładnie tak samo jak w I sposobie otrzymujemy układ równań

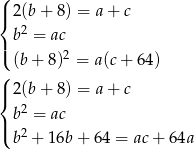
( |{ 2(b + 8 ) = a+ c 2 | b = ac ( (b + 8)2 = a (c+ 6 4) ( |{ 2(b + 8 ) = a+ c b2 = ac |( 2 b + 16b + 6 4 = ac+ 64a

Odejmujemy od trzeciego równania drugie (żeby skrócić kwadraty) i mamy

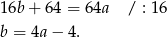
1 6b+ 64 = 64a / : 16 b = 4a− 4.

Podstawiamy to wyrażenie do pierwszego równania układu i mamy

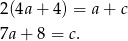
2(4a + 4 ) = a+ c 7a + 8 = c.

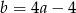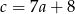Podstawiamy teraz b = 4a − 4 i c = 7a+ 8 do drugiego równania układu.

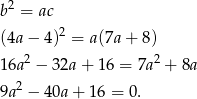
2 b = ac (4a − 4 )2 = a(7a + 8) 2 2 1 6a − 32a+ 16 = 7a + 8a 9a 2 − 4 0a+ 16 = 0.

Dalej postępujemy dokładnie tak samo jak w sposobie I.  
Odpowiedź: 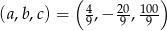( ) (a,b,c) = 49,− 209 , 1090 lub (a,b,c) = (4 ,12,36)

Wersja PDF