/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 8683688

Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 45. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o 3 to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.

Wersja PDF

Rozwiązanie

Oznaczmy szukane liczby przez 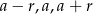a − r,a,a + r . Wtedy z podanej sumy mamy

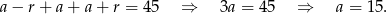
a − r + a + a + r = 45 ⇒ 3a = 45 ⇒ a = 15.

Zatem szukamy liczb postaci 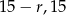15− r,15 i 15 + r .

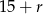Wiemy ponadto, że liczby 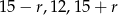1 5− r,1 2,15+ r są kolejnymi wyrazami ciągu geometrycznego, czyli

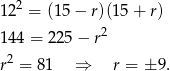
12 2 = (15− r)(15+ r) 2 14 4 = 225 − r r2 = 8 1 ⇒ r = ± 9.

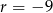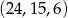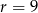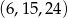Dla r = − 9 mamy ciąg (24,15,6) , a dla r = 9 ciąg (6,15,24) .  
Odpowiedź: (24 ,1 5,6),(6,15,24)

Wersja PDF