/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Różne

Zadanie nr 1546210

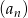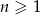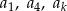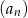W nieskończonym ciągu arytmetycznym (an) , określonym dla n ≥ 1 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy a , a , a 1 4 k ciągu (an) , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 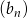(bn) . Oblicz k .

Wersja PDF

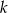Rozwiązanie

Z podanych informacji o ciągu arytmetycznym otrzymujemy układ równań

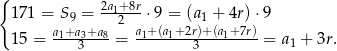
{ 2a+ 8r 171 = S 9 = --12---⋅9 = (a 1 + 4r) ⋅9 15 = a1+a3+a8 = a1+-(a1+2r)+(a1+-7r)-= a + 3r . 3 3 1

Podstawiamy teraz 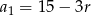a1 = 15 − 3r z drugiego równania do pierwszego.

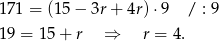
171 = (1 5− 3r+ 4r )⋅9 / : 9 19 = 15 + r ⇒ r = 4.

Mamy stąd 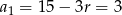a1 = 15 − 3r = 3 , więc

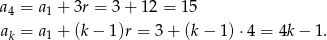
a4 = a1 + 3r = 3 + 12 = 15 a = a1 + (k− 1)r = 3+ (k− 1)⋅4 = 4k− 1. k

Wiemy, że liczby 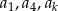a ,a ,a 1 4 k tworzą ciąg geometryczny, więc

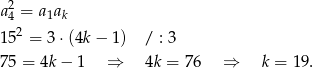
a2= a a 4 1 k 152 = 3 ⋅(4k− 1) / : 3 75 = 4k − 1 ⇒ 4k = 76 ⇒ k = 1 9.

 
Odpowiedź: k = 1 9

Wersja PDF