Zadanie nr 5558016
W ciągu arytmetycznym wyraz pierwszy jest równy 1, a ostatni 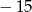 . Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
. Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
Rozwiązanie
Korzystając ze wzoru na  –ty wyraz ciągu arytmetycznego mamy
–ty wyraz ciągu arytmetycznego mamy
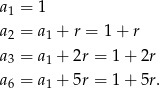
Wiemy, że 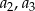 i
i 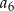 są kolejnymi wyrazami ciągu geometrycznego, zatem
są kolejnymi wyrazami ciągu geometrycznego, zatem
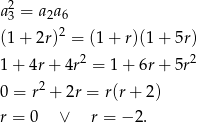
Gdyby 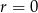 to ciąg byłby stały i ostatni wyraz nie mógłby być równy
to ciąg byłby stały i ostatni wyraz nie mógłby być równy 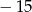 . Zatem
. Zatem 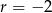 . Obliczmy jaki jest numer ostatniego wyrazu.
. Obliczmy jaki jest numer ostatniego wyrazu.
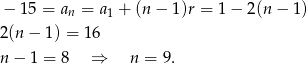
Liczymy sumę wyrazów ciągu
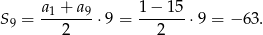
Odpowiedź: