/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Różne

Zadanie nr 6725887

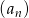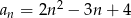Ciąg (an) określony jest wzorem 2 an = 2n − 3n + 4 .

  • Trzeci i piąty wyraz ciągu 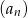(an) są odpowiednio równe szóstemu i dziewiętnastemu wyrazowi ciągu arytmetycznego 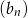(bn ) . Ile początkowych wyrazów ciągu arytmetycznego 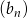(b ) n należy dodać, aby otrzymana suma była nie mniejsza od 483?
  • Piąty oraz trzeci wyraz ciągu 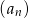(an) są odpowiednio równe pierwszemu i drugiemu wyrazowi nieskończonego ciągu geometrycznego 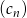(cn) . Który wyraz ciągu 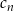c n jest równy 13 9 ?
Wersja PDF

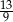Rozwiązanie

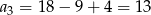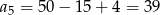  • Ponieważ a3 = 18− 9+ 4 = 13 i a5 = 5 0− 15+ 4 = 39 mamy
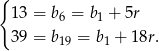
    { 1 3 = b6 = b1 + 5r 3 9 = b19 = b1 + 18r.

    Odejmując od drugiego równania pierwsze (żeby skrócić 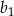b1 ) mamy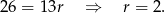

    26 = 13r ⇒ r = 2.

    Zatem 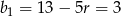b1 = 13 − 5r = 3 . Na mocy wzoru na sumę wyrazów ciągu arytmetycznego mamy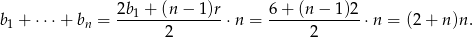

    2b-1 +-(n-−-1-)r 6-+-(n-−-1)2- b1 + ⋅⋅⋅+ bn = 2 ⋅n = 2 ⋅n = (2+ n)n.

    Pozostało rozwiązać nierówność

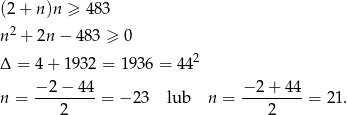
    (2+ n)n ≥ 4 83 n2 + 2n − 483 ≥ 0 2 Δ = 4+ 1932 = 19 36 = 44 −2 − 4 4 − 2+ 44 n = ---------= − 23 lub n = ---------= 2 1. 2 2

    Ponieważ 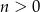n > 0 , mamy stąd n ≥ 21 .  
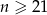    Odpowiedź: Co najmniej 21 wyrazów.

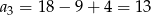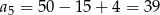  • Ponieważ a3 = 18− 9+ 4 = 13 i a5 = 5 0− 15+ 4 = 39 , mamy
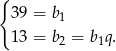
    { 39 = b 1 13 = b2 = b1q.

    Dzieląc drugą równość przez pierwszą mamy

    1-= q. 3

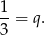
    Mamy zatem równanie

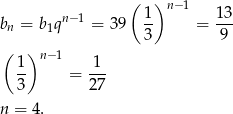
    ( )n− 1 bn = b1qn−1 = 39 1- = 13- 3 9 ( )n −1 1- = 1-- 3 27 n = 4.

     
    Odpowiedź: Czwarty wyraz.

Wersja PDF