/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Różne

Zadanie nr 9714676

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg arytmetyczny 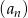(an ) o różnicy 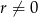r ⁄= 0 i pierwszym wyrazie 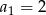a1 = 2 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.

Rozwiązanie

Wiemy, że liczby

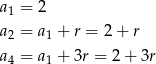
a = 2 1 a2 = a1 + r = 2 + r a = a + 3r = 2+ 3r 4 1

są kolejnymi wyrazami ciągu geometrycznego. W takim razie kwadrat środkowej z tych liczb musi być iloczynem dwóch pozostałych.

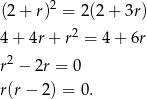
2 (2+ r) = 2(2 + 3r) 4+ 4r+ r2 = 4+ 6r 2 r − 2r = 0 r(r− 2) = 0.

Ponieważ z założenia 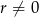r ⁄= 0 , mamy 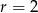r = 2 i interesujący nas iloraz jest równy

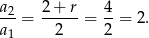
a 2+ r 4 -2-= -----= --= 2. a1 2 2

 
Odpowiedź: 2

Wersja PDF