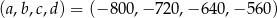Zadanie nr 1920022
Czterowyrazowy ciąg 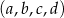 jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg
jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg 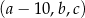 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 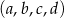 .
.
Rozwiązanie
Jeżeli oznaczymy przez  różnicę danego ciągu, to
różnicę danego ciągu, to 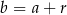 ,
, 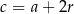 oraz
oraz 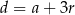 . Pozostałe podane informacje prowadzą do układu równań
. Pozostałe podane informacje prowadzą do układu równań
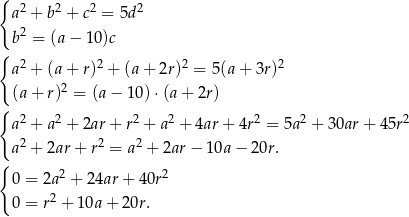
Drugie równanie na chwilę zostawmy tak jak jest, a pierwsze podzielmy stronami przez 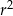 – możemy to zrobić, bo wiemy, że ciąg jest rosnący, czyli
– możemy to zrobić, bo wiemy, że ciąg jest rosnący, czyli 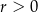 .
.
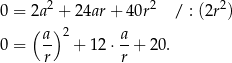
Podstawiamy teraz 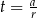 .
.
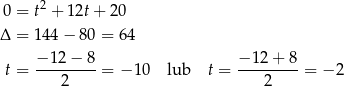
Zatem 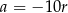 lub
lub 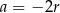 . Załóżmy najpierw, że
. Załóżmy najpierw, że 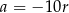 . Podstawiamy to wyrażenie do drugiego równania układu.
. Podstawiamy to wyrażenie do drugiego równania układu.
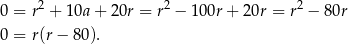
Interesują nas tylko dodatnie wartości  (bo ciąg ma być rosnący), więc mamy stąd
(bo ciąg ma być rosnący), więc mamy stąd 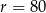 ,
, 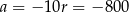 i
i
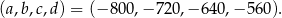
Pozostał jeszcze do rozpatrzenia drugi przypadek, gdy 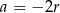 . Tak jak poprzednio podstawiamy to wyrażenie do drugiego równania układu.
. Tak jak poprzednio podstawiamy to wyrażenie do drugiego równania układu.
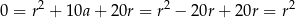
Ponieważ interesują nas tylko dodatnie wartości  , w tym przypadku nie otrzymamy nowych rozwiązań.
, w tym przypadku nie otrzymamy nowych rozwiązań.
Odpowiedź: