Zadanie nr 2147450
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Rozwiązanie
Oznaczmy podane liczby przez 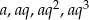 . Wiemy więc, że ciąg
. Wiemy więc, że ciąg 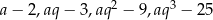 jest arytmetyczny. Zatem zarówno druga jak i trzecia liczba jest średnią arytmetyczną sąsiednich. Daje nam to układ równań.
jest arytmetyczny. Zatem zarówno druga jak i trzecia liczba jest średnią arytmetyczną sąsiednich. Daje nam to układ równań.
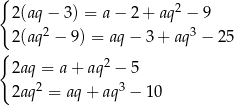
Musimy jakoś rozwiązać ten układ równań. Widać, że ciężko będzie wyeliminować 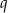 , pokombinujmy zatem z
, pokombinujmy zatem z  . Można po prostu wyliczyć
. Można po prostu wyliczyć  z pierwszego równania i podstawić do drugiego, prościej jest jednak zauważyć, że współczynniki przy
z pierwszego równania i podstawić do drugiego, prościej jest jednak zauważyć, że współczynniki przy  są w obu równaniach prawie takie same – jedyna różnica, to, że w drugim równaniu są przemnożone dodatkowo przez
są w obu równaniach prawie takie same – jedyna różnica, to, że w drugim równaniu są przemnożone dodatkowo przez 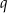 . Odejmijmy zatem od drugiego równania pierwsze przemnożone przez
. Odejmijmy zatem od drugiego równania pierwsze przemnożone przez 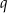 .
.
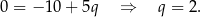
Z pierwszego równania mamy więc
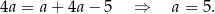
Odpowiedź: 5,10,20,40

