/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Czterowyrazowy

Zadanie nr 2869286

Między liczby 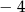− 4 i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.

Wersja PDF

Rozwiązanie

Sposób I

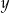Powiedzmy, że wstawione liczby to x i y . Z własności ciągu arytmetycznego i geometrycznego otrzymujemy układ równań

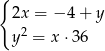
{ 2x = − 4 + y y2 = x ⋅36

Podstawiamy 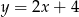y = 2x + 4 z pierwszego równania do drugiego.

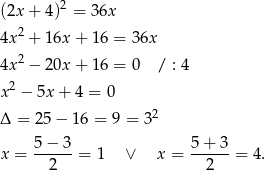
(2x + 4)2 = 36x 4x2 + 16x + 16 = 36x 2 4x − 20x + 16 = 0 / : 4 x2 − 5x + 4 = 0 2 Δ = 25− 16 = 9 = 3 5 − 3 5+ 3 x = ------= 1 ∨ x = ------= 4 . 2 2

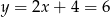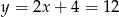Wtedy y = 2x+ 4 = 6 i y = 2x+ 4 = 12 odpowiednio.

Sposób II

Oznaczmy pierwsze trzy liczby przez 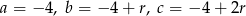a = − 4, b = − 4+ r, c = − 4 + 2r , a trzy ostatnie przez

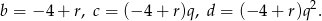
b = − 4 + r, c = (− 4+ r)q, d = (−4 + r)q2.

W szczególności

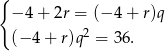
{ − 4 + 2r = (− 4 + r)q (− 4 + r)q2 = 36 .

Jeżeli 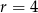r = 4 , to drugie równanie przyjmuje postać 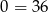0 = 36 , co oczywiście nie jest możliwe. Zatem 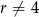r ⁄= 4 i z pierwszego równania możemy wyliczyć 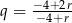−4+2r- q = − 4+r . Podstawiamy tę wartość do drugiego równania.

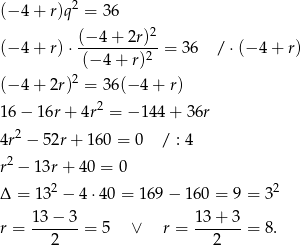
(− 4 + r)q2 = 36 (−-4+--2r)2 (− 4 + r) ⋅ (− 4 + r)2 = 36 / ⋅(− 4+ r) 2 (− 4 + 2r) = 3 6(− 4+ r) 2 16 − 1 6r+ 4r = − 144+ 36r 4r2 − 52r + 16 0 = 0 / : 4 2 r − 13r + 40 = 0 Δ = 132 − 4 ⋅40 = 1 69− 160 = 9 = 32 r = 13−--3-= 5 ∨ r = 13-+-3-= 8. 2 2

Mamy wtedy odpowiednio

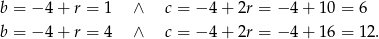
b = − 4 + r = 1 ∧ c = − 4+ 2r = − 4+ 10 = 6 b = − 4 + r = 4 ∧ c = − 4+ 2r = − 4+ 16 = 12.

 
Odpowiedź: Należy wstawić liczby 1 i 6 lub 4 i 12.

Wersja PDF