Zadanie nr 4357833
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 14, a suma drugiej i trzeciej wynosi 12. Wyznacz te 4 liczby.
Rozwiązanie
Oznaczmy szukane liczby przez 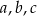 i
i 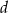 .
.
Sposób I
Pierwsze trzy tworzą ciąg geometryczny, więc 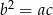 , ostatnie trzy arytmetyczny, czyli
, ostatnie trzy arytmetyczny, czyli 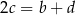 . Otrzymujemy układ równań
. Otrzymujemy układ równań
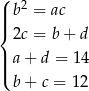
Z ostatniego równania obliczamy 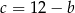 a z przedostatniego
a z przedostatniego 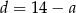 i podstawiamy do dwóch pierwszych równań
i podstawiamy do dwóch pierwszych równań
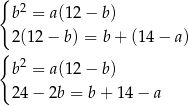
Z drugiego równania mamy 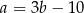 . Wstawiamy to do pierwszego równania.
. Wstawiamy to do pierwszego równania.
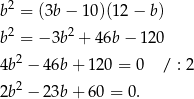
Rozwiązujemy otrzymane równanie kwadratowe,
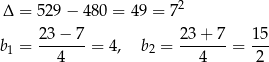
Jeżeli 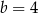 , to
, to
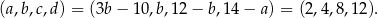
Jeżeli natomiast 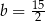 , to
, to
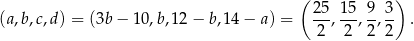
Sposób II
Jeżeli oznaczmy przez 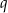 iloraz ciągu geometrycznego, to wiemy, że
iloraz ciągu geometrycznego, to wiemy, że 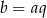 i
i 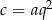 . Ponadto
. Ponadto
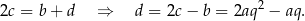
Mamy zatem układ równań
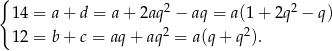
Dzielimy teraz pierwsze równanie stronami przez drugie (możemy to zrobić bo w obu równaniach obie strony są niezerowe – w pierwszym równe 14, a w drugim 12).
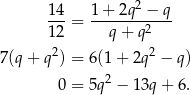
Rozwiązujemy otrzymane równanie kwadratowe
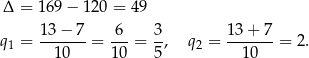
Mamy wtedy
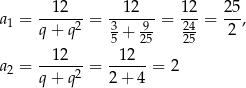
odpowiednio. W pierwszym przypadku otrzymujemy ciąg
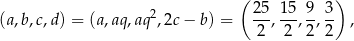
a w drugim przypadku
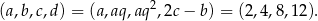
Odpowiedź: 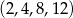 lub
lub