Zadanie nr 6800562
Liczby 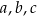 są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby
są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby 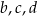 są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby
są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby 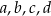 .
.
Rozwiązanie
Sposób I
Mamy równania
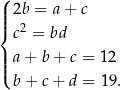
Z pierwszego równania wyliczamy 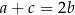 i podstawiamy do trzeciego równania
i podstawiamy do trzeciego równania

Pozostaje nam więc układ
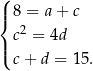
Podstawiając z trzeciego równania 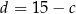 do drugiego mamy
do drugiego mamy
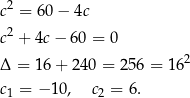
Mamy wtedy odpowiednio
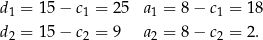
Sposób II
Wiemy, że 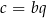 i
i 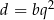 oraz
oraz
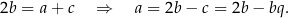
Mamy zatem układ równań
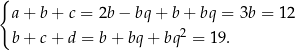
Z pierwszego równania mamy natychmiast 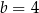 i drugie równanie przyjmuje postać
i drugie równanie przyjmuje postać
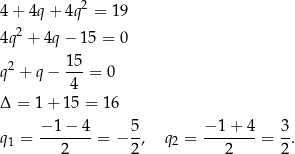
Stąd mamy odpowiednio
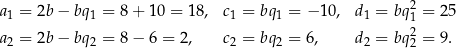
Odpowiedź: 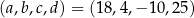 lub
lub