/Szkoła średnia/Ciągi/Szereg geometryczny/Dana suma

Zadanie nr 2361357

Dany jest nieskończony ciąg geometryczny 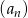(an) określony dla 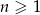n ≥ 1 , w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału 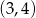(3,4) . Oblicz iloraz tego ciągu.

Wersja PDF

Rozwiązanie

Oznaczmy przez 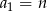a1 = n pierwszy wyraz ciągu. Wtedy trzeci wyraz jest równy 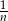n1 , więc

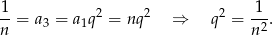
1- = a3 = a1q 2 = nq2 ⇒ q2 = 1-. n n2

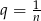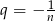To oznacza, że 1 q = n lub 1 q = − n . W pierwszym przypadku suma wszystkich wyrazów ciągu jest równa

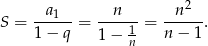
2 S = --a1--= --n---= --n---. 1 − q 1 − 1 n − 1 n

Mamy zatem nierówność

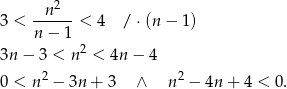
n 2 3 < ------< 4 / ⋅(n − 1) n − 1 2 3n − 3 < n < 4n − 4 2 2 0 < n − 3n + 3 ∧ n − 4n + 4 < 0.

Zauważmy, że druga z powyższych nierówności jest sprzeczna, bo 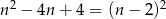n 2 − 4n + 4 = (n − 2)2 .

W takim razie musi być 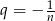q = − 1n i suma szeregu jest równa

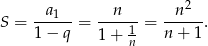
--a1-- --n--- --n2-- S = 1 − q = 1 + 1 = n + 1 . n

Mamy zatem nierówność

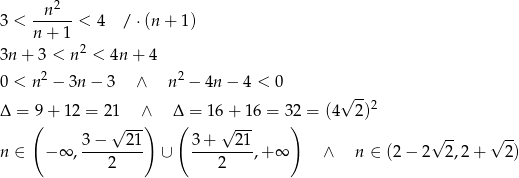
2 3 < -n----< 4 / ⋅(n + 1) n + 1 3n + 3 < n2 < 4n + 4 2 2 0 < n − 3n − 3 ∧ n − 4n − 4 < 0 √ --2 Δ = 9( + 12 = 21√ --∧) Δ(= 16√+-16 = 32) = (4 2) 3− 21 3+ 21 √ -- √ -- n ∈ −∞ , --------- ∪ --------,+ ∞ ∧ n ∈ (2 − 2 2,2 + 2 ) 2 2

Ponieważ 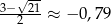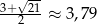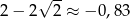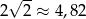√-- 3−-221-≈ − 0 ,7 9 , √-- 3+-221 ≈ 3,79 , √ -- 2− 2 2 ≈ − 0,83 , √ -- 2 2 ≈ 4 ,8 2 , mamy stąd

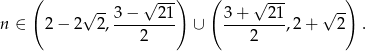
( √ --) ( √ --- ) √ -- 3− 21 3+ 21 √ -- n ∈ 2 − 2 2, --------- ∪ --------,2 + 2 . 2 2

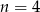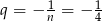Jedyną liczbą naturalną spełniającą ten warunek jest n = 4 . Zatem q = − 1 = − 1 n 4 .  
Odpowiedź: 1 q = − 4

Wersja PDF