/Szkoła średnia/Ciągi/Szereg geometryczny/Na dowodzenie

Zadanie nr 1877917

Dodaj do ulubionych
Dodaj do rozwiązanych

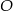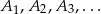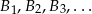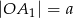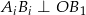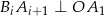Na jednym z ramion kąta ostrego o wierzchołku O i mierze α wybrano punkty A 1,A 2,A3,... , a na drugim ramieniu punkty B1,B 2,B3,... w ten sposób, że |OA 1| = a , AiBi ⊥ OB 1 oraz BiAi +1 ⊥ OA 1 dla wszystkich i ≥ 1 .

PIC

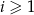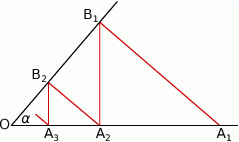
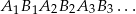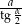Wykaż, że długość nieskończonej łamanej A 1B 1A2B 2A 3B 3... jest równa --aα tg 2 .

Rozwiązanie

Z trójkąta prostokątnego 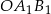OA 1B 1 mamy

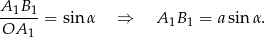
A B --1-1-= sin α ⇒ A 1B1 = asinα . OA 1

Teraz patrzymy na trójkąt prostokątny 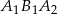A 1B1A 2 (lub ogólniej 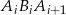AiBiAi +1 ). Ponieważ 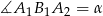∡A 1B 1A2 = α (lub ogólnie 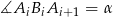∡AiBiAi +1 = α ) mamy

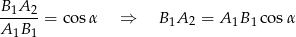
B1A-2-= co sα ⇒ B 1A 2 = A 1B1co sα A 1B1

(ogólnie 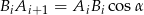BiAi+1 = AiBico sα ).

Podobnie, z trójkąta prostokątnego 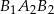B 1A 2B2 (lub ogólnie 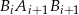BiAi +1Bi+ 1 ) mamy

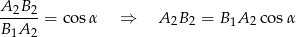
A-2B2- B1A 2 = co sα ⇒ A 2B 2 = B1A 2co sα

(ogólnie 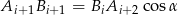A B = B A cos α i+1 i+ 1 i i+ 2 ).

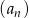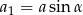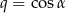To oznacza, że kolejne odcinki łamanej są kolejnymi wyrazami ciągu geometrycznego (an) , w którym a1 = asinα i q = cos α . Suma tego ciągu jest równa

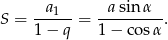
S = --a1--= -a-sin-α--. 1 − q 1− cosα

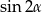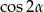Teraz korzystamy ze wzorów na sin 2α i cos2α .

-asin-α-- --2a-sin-α2-cos-α2--- 2asin-α2 co-s α2 a-cos α2 --a-- --a- S = 1− c osα = 2 α = 2 α = sin α = -sin α2 = tg α. 1 − (1 − 2sin 2) 2 sin 2 2 cos α2 2
Wersja PDF