/Szkoła średnia/Ciągi/Szereg geometryczny/Na dowodzenie

Zadanie nr 5739211

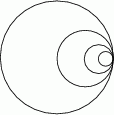
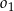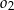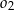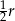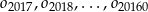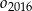Dany jest okrąg o1 o promieniu r . Wewnątrz tego okręgu narysowano okrąg o2 styczny wewnętrznie o średnicy r , wewnątrz okręgu o 2 znów narysowano okrąg styczny wewnętrznie o średnicy 12r itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów o2017,o2018,...,o20160 jest mniejsza od długości okręgu o2016 .

PIC

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy przez 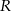R promień okręgu 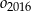o2016 , to jego długość jest równa

S = 2πR .

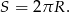
Zauważmy teraz, że każdy kolejny okrąg ma promień dwa razy mniejszy od poprzedniego, więc sumę długości wszystkich okręgów o numerach większych od 2016 możemy obliczyć jako sumę szeregu geometrycznego 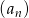(an) o pierwszym wyrazie 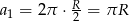a = 2π ⋅ R-= πR 1 2 i ilorazie 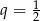q = 1 2 . Suma ta jest więc równa

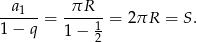
a1 πR ------= -----1= 2πR = S. 1− q 1 − 2

Suma długości okręgów 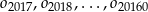o2017,o2018,...,o20160 jest oczywiście mniejsza.

Wersja PDF