Zadanie nr 2842513

Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego (wszystkie składniki szeregu są różne od zera)

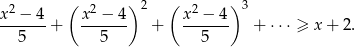
( ) 2 ( ) 3 x2 −-4- x2-−-4- x2 −-4- 5 + 5 + 5 + ⋅⋅⋅ ≥ x+ 2.

Rozwiązanie

Sprawdźmy najpierw, kiedy szereg geometryczny o ilorazie 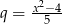x2−-4 q = 5 jest zbieżny. Rozwiązujemy nierówność

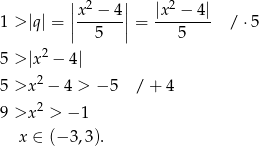
| 2 | 2 1 > |q| = ||x-−--4|| = |x--−-4| / ⋅ 5 | 5 | 5 2 5 > |x − 4| 5 >x 2 − 4 > − 5 / + 4 2 9 >x > − 1 x ∈ (− 3,3).

Mamy dodatkowo w treści założenie, że wyrazy ciągu geometrycznego są niezerowe, więc dodatkowo 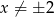x ⁄= ± 2 .

Teraz liczymy sumę szeregu

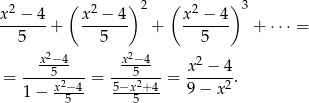
( ) 2 ( ) 3 x2-−-4- x2-−-4- x2-−-4- 5 + 5 + 5 + ⋅⋅⋅ = 2 2 --x-−54--- --x−5-4- x2 −-4- = x2−4 = 5−x-2+-4 = 9− x 2. 1 − 5 5

Pozostało więc rozwiązać nierówność

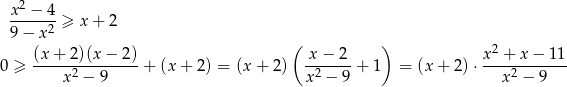
x2 − 4 -------≥ x+ 2 9 − x2 ( ) (x + 2)(x − 2) x − 2 x2 + x− 11 0 ≥ ----x-2 −-9----+ (x+ 2) = (x + 2) x2 −-9 + 1 = (x+ 2)⋅ --x-2 −-9---

Zauważmy w tym miejscu, że założyliśmy wyżej, że 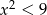x2 < 9 , więc powyższa nierówność jest równoważna nierówności

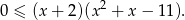
0 ≤ (x+ 2)(x2 + x− 11).

Rozłóżmy jeszcze trójmian w drugim nawiasie.

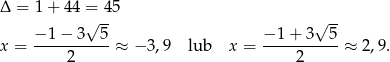
Δ = 1 + 44 = 4 5 √ -- √ -- x = −-1−--3--5-≈ −3 ,9 lub x = −-1-+-3--5-≈ 2,9. 2 2

A zatem dana nierówność sprowadza się do

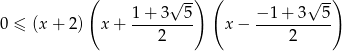
( √ --) ( √ --) 1-+-3--5- −-1-+-3--5- 0 ≤ (x+ 2) x + 2 x − 2

Jej rozwiązaniem jest zbiór

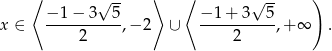
⟨ √ -- ⟩ ⟨ √ -- ) x ∈ −1-−-3---5,− 2 ∪ −1-+-3---5,+ ∞ . 2 2

W połączeniu z wcześniej trzymanymi warunkami na 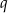, dostajemy zbiór rozwiązań:

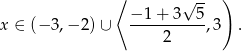
⟨ √ -- ) x ∈ (−3 ,−2 )∪ −-1-+-3--5-,3 . 2

Odpowiedź: ⟨ - ) −1+3√-5 x ∈ (− 3,− 2) ∪ 2 ,3