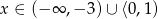Zadanie nr 3235592
Rozwiąż nierówność
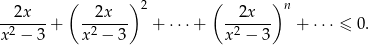
Rozwiązanie
Musimy najpierw ustalić jaka jest dziedzina lewej strony (szereg musi być zbieżny).
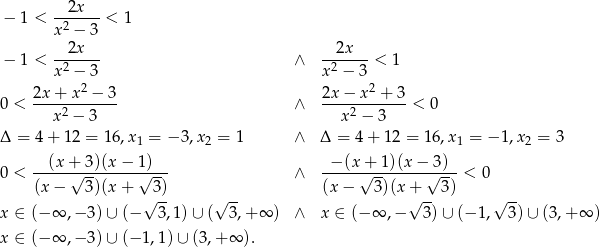
Ze wzoru na sumę szeregu geometrycznego 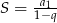 mamy nierówność
mamy nierówność
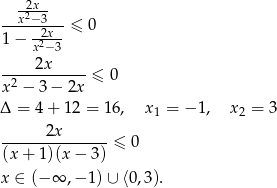
Łącząc oba otrzymane warunki, dostajemy
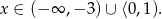
Odpowiedź: 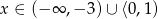
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność
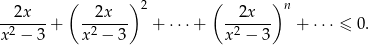
Musimy najpierw ustalić jaka jest dziedzina lewej strony (szereg musi być zbieżny).
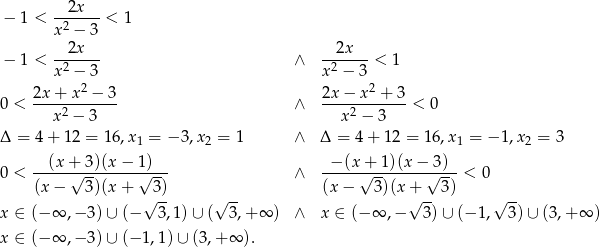
Ze wzoru na sumę szeregu geometrycznego 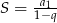 mamy nierówność
mamy nierówność
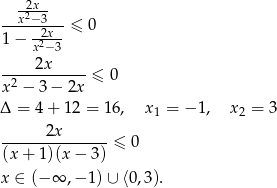
Łącząc oba otrzymane warunki, dostajemy
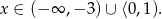
Odpowiedź: