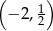/Szkoła średnia/Nierówności/Z kropkami

Zadanie nr 6712093

Rozwiąż nierówność

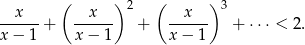
( ) 2 ( )3 --x---+ --x--- + --x--- + ⋅⋅⋅ < 2. x − 1 x − 1 x − 1
Wersja PDF

Rozwiązanie

Po pierwsze musimy sprawdzić kiedy podany szereg jest zbieżny, czyli rozwiązujemy nierówność

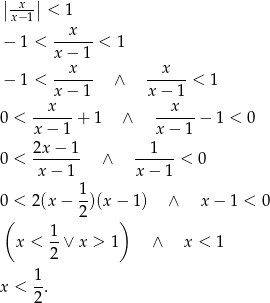
||-x-|| x−1 < 1 --x--- − 1 < x − 1 < 1 x x − 1 < ------ ∧ ------< 1 xx − 1 x− x1 0 < ------+ 1 ∧ ------− 1 < 0 x − 1 x− 1 2x-−-1- --1--- 0 < x− 1 ∧ x − 1 < 0 1 0 < 2(x − --)(x− 1) ∧ x − 1 < 0 ( 2 ) 1- x < 2 ∨ x > 1 ∧ x < 1 x < 1-. 2

Teraz liczymy sumę szeregu

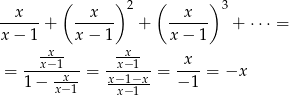
( ) 2 ( ) 3 --x---+ --x--- + --x--- + ⋅⋅ ⋅ = x − 1 x− 1 x − 1 -x-- -x-- x = --x−1x--= -x−-1--= ----= −x 1− x−1- x−x1−−x1- − 1

A zatem dana nierówność sprowadza się do

−x < 2 ⇒ x > − 2.

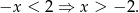
W połączeniu z wcześniej wyliczonym warunkiem na 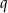q , dostajemy zbiór rozwiązań ( ) − 2, 12 .  
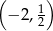Odpowiedź: ( ) − 2, 12

Wersja PDF