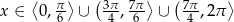Zadanie nr 7785616
Rozwiąż nierówność 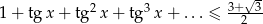 w zbiorze
w zbiorze 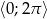 .
.
Rozwiązanie
Aby lewa strona była zbieżnym szeregiem geometrycznym musimy mieć 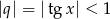 . Mamy wtedy
. Mamy wtedy
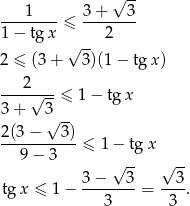
Uwzględniając założenie 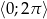 oraz warunek
oraz warunek 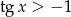 daje to nam
daje to nam
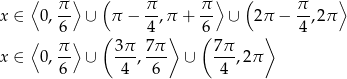
Odpowiedź: 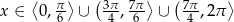
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 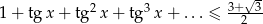 w zbiorze
w zbiorze 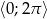 .
.
Aby lewa strona była zbieżnym szeregiem geometrycznym musimy mieć 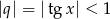 . Mamy wtedy
. Mamy wtedy
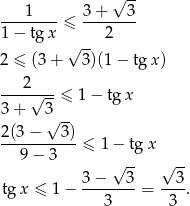
Uwzględniając założenie 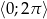 oraz warunek
oraz warunek 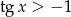 daje to nam
daje to nam
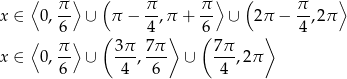
Odpowiedź: