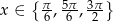Zadanie nr 9404528
Rozwiąż nierówność 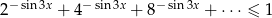 , gdzie
, gdzie 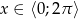 .
.
Rozwiązanie
Jeżeli zapiszemy nierówność w postaci
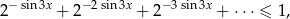
to widać, że lewa strona jest zbieżnym szeregiem geometrycznym, o ile
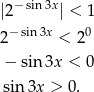
Mamy wtedy nierówność
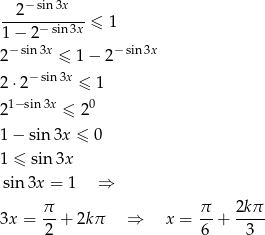
Uwzględniając podany przedział otrzymujemy
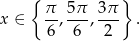
Odpowiedź: 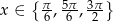
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 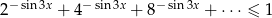 , gdzie
, gdzie 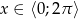 .
.
Jeżeli zapiszemy nierówność w postaci
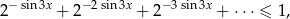
to widać, że lewa strona jest zbieżnym szeregiem geometrycznym, o ile
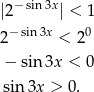
Mamy wtedy nierówność
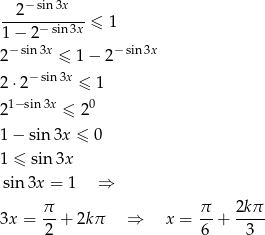
Uwzględniając podany przedział otrzymujemy
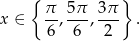
Odpowiedź: