/Szkoła średnia/Nierówności/Z kropkami

Zadanie nr 9516785

Rozwiąż nierówność

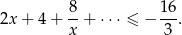
8 16 2x+ 4+ --+ ⋅⋅⋅ ≤ − ---. x 3
Wersja PDF

Rozwiązanie

Po pierwsze musimy sprawdzić kiedy szereg geometryczny z lewej strony nierówności jest zbieżny. Oczywiście musi być 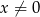x ⁄= 0 . Ponadto jest to szereg o ilorazie 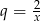q = 2x , więc musi być spełniona nierówność

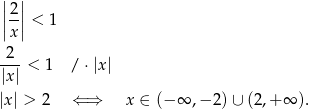
| | ||2-||< 1 |x | 2 --- < 1 /⋅ |x | |x| |x | > 2 ⇐ ⇒ x ∈ (− ∞ ,− 2) ∪ (2,+ ∞ ).

Przy tym założeniu możemy skorzystać ze wzoru na sumę szeregu geometrycznego.

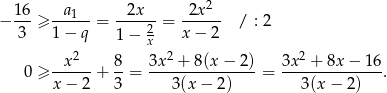
16 a 2x 2x 2 − ---≥ --1---= ------ = ------ / : 2 3 1− q 1 − 2x x − 2 x 2 8 3x2 + 8(x − 2) 3x2 + 8x − 1 6 0 ≥ ------+ --= ---------------= --------------. x− 2 3 3(x − 2) 3(x − 2)

Rozłóżmy trójmian w liczniku tego ułamka.

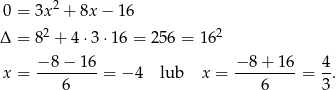
2 0 = 3x + 8x − 16 Δ = 82 + 4⋅3 ⋅16 = 256 = 16 2 x = −-8-−-16-= −4 lub x = −-8-+-16-= 4. 6 6 3

Powyższa nierówność jest więc równoważna nierówności

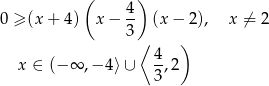
( ) 0 ≥ (x + 4) x− 4- (x − 2), x ⁄= 2 3 ⟨ ) x ∈ (− ∞ ,− 4⟩∪ 4,2 3

W połączeniu z wcześniej wyliczonym warunkiem na 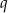q , dostajemy zbiór rozwiązań (− ∞ ,− 4⟩ .  
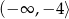Odpowiedź: (− ∞ ,− 4⟩

Wersja PDF