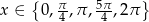/Szkoła średnia/Równania/Trygonometryczne/Stopnia 2

Zadanie nr 1196806

Wyznacz wszystkie rozwiązania równania 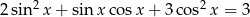2 2 2sin x+ sin x cosx + 3 cos x = 3 należące do przedziału ⟨0,2π ⟩ .

Wersja PDF

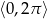Rozwiązanie

Przekształcamy (korzystając z jedynki trygonometrycznej).

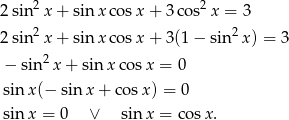
2 2 2 sin x + sinx cos x+ 3co s x = 3 2 sin 2x + sinx cos x+ 3(1− sin 2x) = 3 2 − sin x + sin xco sx = 0 sin x(− sin x + cos x) = 0 sin x = 0 ∨ sin x = co sx.

Rozwiązaniem pierwszego równania (w danym przedziale) są liczby 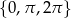{0 ,π,2π } , a drugie równanie możemy przekształcić następująco:

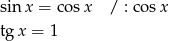
sin x = co sx / : cosx tg x = 1

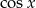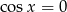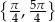(dzieliliśmy przez co sx , bo widać, że jeżeli cos x = 0 to równanie jest sprzeczne). Mamy stąd dwa dodatkowe rozwiązania: { π- 5π} 4 ,4 .  
Odpowiedź: { } x ∈ 0, π4-,π, 5π4-,2π

Wersja PDF