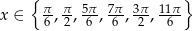/Szkoła średnia/Równania/Trygonometryczne/Stopnia 2

Zadanie nr 1853170

Rozwiąż równanie 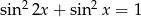2 2 sin 2x + sin x = 1 w zbiorze ⟨0,2π ⟩ .

Wersja PDF

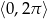Rozwiązanie

Sposób I

Korzystamy ze wzoru

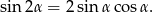
sin 2α = 2 sinα cos α.

Mamy zatem

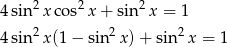
4 sin2x cos2x + sin2 x = 1 4 sin2x(1 − sin2 x)+ sin 2x = 1

Podstawiamy teraz 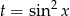2 t = sin x .

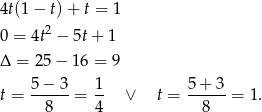
4t(1 − t)+ t = 1 0 = 4t2 − 5t+ 1 Δ = 25 − 16 = 9 5-−-3- 1- 5+--3- t = 8 = 4 ∨ t = 8 = 1.

Stąd

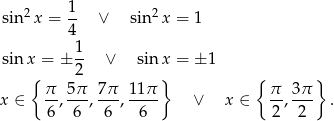
1 sin2 x = -- ∨ sin2x = 1 4 sin x = ± 1- ∨ sinx = ± 1 { 2 } { } π 5π 7π 11π π 3π x ∈ --,---, ---,---- ∨ x ∈ --,--- . 6 6 6 6 2 2

Sposób II

Tym razem skorzystamy ze wzoru

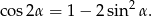
2 cos2α = 1− 2sin α.

Mamy więc

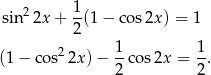
1 sin 22x + -(1 − cos2x ) = 1 2 2 1- 1- (1 − co s 2x) − 2 cos 2x = 2.

Podstawiamy teraz 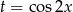t = cos2x .

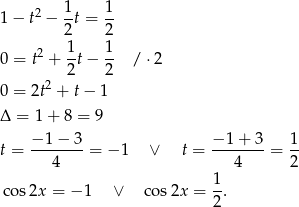
1 1 1 − t2 − --t = -- 2 2 0 = t2 + 1t− 1- / ⋅ 2 2 2 0 = 2t2 + t − 1 Δ = 1 + 8 = 9 − 1− 3 − 1 + 3 1 t = ------- = − 1 ∨ t = ------- = -- 4 4 2 cos2x = − 1 ∨ cos 2x = 1. 2

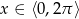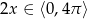Teraz trzeba odrobinę uważać, bo wprawdzie x ∈ ⟨0,2π ⟩ , ale 2x ∈ ⟨0,4π ⟩ . Stąd

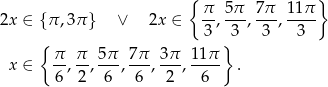
{ } 2x ∈ {π ,3π} ∨ 2x ∈ π-, 5π-, 7π-, 11π 3 3 3 3 { π π 5π 7π 3π 11π } x ∈ --,--,---,---,---, ---- . 6 2 6 6 2 6

Sposób III

Przekształcamy dane równanie korzystając z jedynki trygonometrycznej i wzoru na 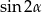sin 2α .

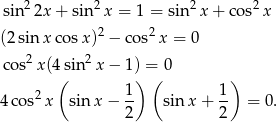
2 2 2 2 sin 2x + sin x = 1 = sin x + co s x (2sin xco sx)2 − cos2 x = 0 2 2 co s x(4(sin x − 1)) =(0 ) 2 1 1 4 cos x sin x − -- sin x+ -- = 0. 2 2

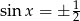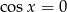Stąd 1 sin x = ± 2 lub co sx = 0 , czyli

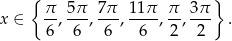
{ π 5π 7 π 11π π 3π } x ∈ --,---,--- ,----,--,--- . 6 6 6 6 2 2

 
Odpowiedź: { } x ∈ π6-, π2, 5π6-, 7π6 , 3π2-, 116π

Wersja PDF