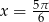/Szkoła średnia/Równania/Trygonometryczne/Stopnia 2

Zadanie nr 2701787

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 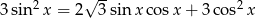2 √ -- 2 3sin x = 2 3 sin x cosx + 3 cos x w przedziale ⟨0,π ⟩ .

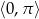Rozwiązanie

Sposób I

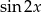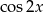Korzystamy ze wzorów na sin2x i cos 2x .

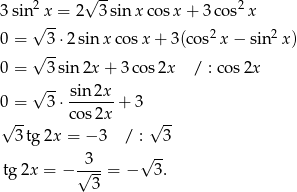
2 √ -- 2 3sin√x-= 2 3 sin x cosx + 3 cos x 0 = 3 ⋅2sin xco sx + 3(cos2 x− sin 2x) √ -- 0 = 3 sin 2x + 3 cos2x / : co s2x √ -- sin2x 0 = 3 ⋅-------+ 3 √ -- cos 2x √ -- 3tg 2x = − 3 / : 3 3 √ -- tg2x = − √---= − 3. 3

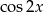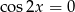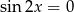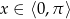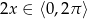Dwie sprawy: dzieliliśmy po drodze przez cos 2x – nie ma z tym problemu, bo gdyby cos2x = 0 , to z trzeciej linijki powyższych przekształceń mamy sin 2x = 0 , co nie jest możliwe (ze względu np. na jedynkę trygonometryczną). Druga sprawa to przestroga – wprawdzie x ∈ ⟨0,π⟩ , ale 2x ∈ ⟨0,2π⟩ .

PIC

Są zatem dwa kąty spełniające powyższą równość:

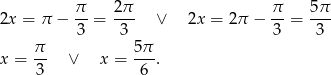
2x = π − π-= 2π- ∨ 2x = 2π − π- = 5π- 3 3 3 3 π- 5π- x = 3 ∨ x = 6 .

Sposób II

Podzielmy dane równanie stronami przez 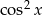cos2 x – dzięki temu otrzymamy same tangensy. Zauważmy jeszcze, że gdyby 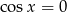cosx = 0 to z równania otrzymujemy 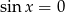sin x = 0 , co nie jest możliwe. Zatem dzielenie przez 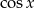cosx nie zmniejsza zbioru rozwiązań.

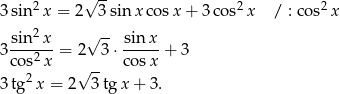
√ -- 3sin2 x = 2 3 sin x cosx + 3 cos2x / : co s2x 2 √ -- 3sin--x = 2 3⋅ sin-x-+ 3 cos2 x √ -- cosx 3tg2 x = 2 3 tgx + 3.

Podstawmy teraz 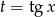t = tgx .

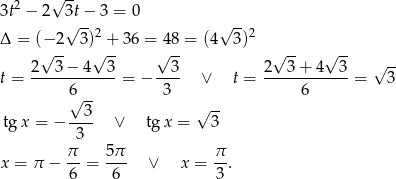
√ -- 3t2 − 2 3t− 3 = 0 √ -- √ -- Δ = (− 2 3)2 + 36 = 48 = (4 3)2 √ -- √ -- √ -- √ -- √ -- √ -- t = 2--3-−-4--3- = − --3- ∨ t = 2--3-+-4--3-= 3 6 -- 3 6 √ 3 √ -- tg x = − ---- ∨ tgx = 3 3 x = π − π- = 5-π ∨ x = π-. 6 6 3

Sposób III

Przekształcamy dane równanie (tym razem skorzystamy ze wzoru na 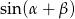sin(α + β) ).

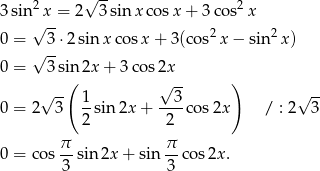
2 √ -- 2 3 sin√ x-= 2 3sinx cos x+ 3co s x 0 = 3 ⋅2 sin x cosx + 3 (cos2x − sin2x ) √ -- 0 = 3 sin2x + 3cos 2x √ -( √ -- ) √ -- 0 = 2 3 1-sin2x + --3-cos2x / : 2 3 2 2 π π 0 = co s-- sin 2x + sin --cos 2x. 3 3

Otrzymane wyrażenie to 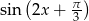( π) sin 2x + 3 , więc otrzymujemy równanie.

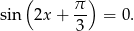
( π-) sin 2x+ 3 = 0 .

Teraz trzeba trochę uważać. Jeżeli 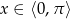x ∈ ⟨0,π ⟩ to

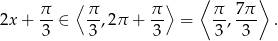
⟨ ⟩ π- ⟨ π- π⟩ π- 7π- 2x + 3 ∈ 3 ,2π + 3 = 3 , 3 .

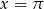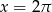W tym przedziale sinus zeruje się dwa razy: dla x = π i x = 2π . Mamy zatem.

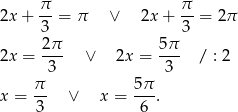
π- π- 2x + 3 = π ∨ 2x + 3 = 2 π 2 π 5 π 2x = --- ∨ 2x = --- / : 2 3 3 x = π- ∨ x = 5π-. 3 6

Sposób IV

Przekształcamy dane równanie.

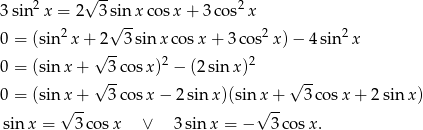
√ -- 3 sin 2x = 2 3sinx cos x+ 3cos2 x 2 √ -- 2 2 0 = (sin x+ 2--3sin xco sx + 3 cos x) − 4 sin x 0 = (sin x+ √ 3co sx)2 − (2sin x)2 √ -- √ -- 0 = (sin x+ 3co sx − 2 sin x)(sinx + 3cos x+ 2sin x) √ -- √ -- sin x = 3 cosx ∨ 3sin x = − 3 cosx.

Zauważmy teraz, że jeżeli 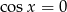co sx = 0 to otrzymujemy sprzeczność, bo wtedy 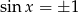sin x = ± 1 , więc możemy podzielić obydwa równania przez cosx .

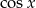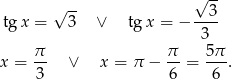
√ -- √ -- 3 tg x = 3 ∨ tg x = − ---- 3 x = π- ∨ x = π − π-= 5π-. 3 6 6

 
Odpowiedź: 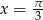x = π3- lub x = 56π-

Wersja PDF