Zadanie nr 5458191

Rozwiąż równanie 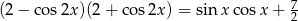7 (2− cos2x )(2+ cos2x ) = sin x cosx + 2 w przedziale ⟨0,π ⟩ .

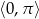Rozwiązanie

Przekształcamy dane równanie korzystając ze wzoru na 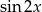sin 2x .

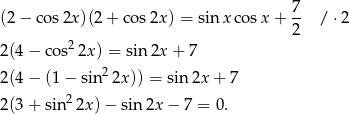
7 (2 − cos 2x)(2 + cos 2x) = sinx cos x+ -- / ⋅2 2 2(4 − cos2 2x) = sin 2x+ 7 2 2(4 − (1 − sin 2x )) = sin2x + 7 2(3 + sin22x )− sin 2x − 7 = 0.

Widać, że możemy teraz podstawić 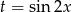t = sin 2x .

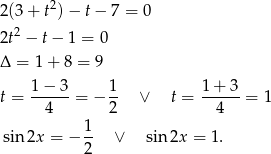
2 (3 + t2) − t− 7 = 0 2 2t − t− 1 = 0 Δ = 1 + 8 = 9 t = 1−--3-= − 1- ∨ t = 1-+-3-= 1 4 2 4 1- sin 2x = − 2 ∨ sin 2x = 1.

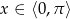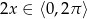Teraz trzeba odrobinę uważać, bo wprawdzie x ∈ ⟨0,π ⟩ , ale 2x ∈ ⟨0,2π⟩ .

Sposób I

Szkicujemy sinusa

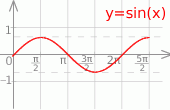
Z wykresu odczytujemy rozwiązania

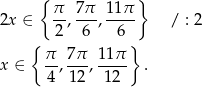
{ } 2x ∈ π-, 7π-, 11π / : 2 2 6 6 { } x ∈ π-, 7-π, 11π . 4 12 1 2

Sposób II

Liczymy

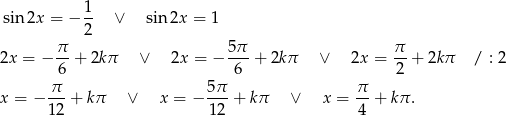
1 sin 2x = − -- ∨ sin 2x = 1 2 2x = − π-+ 2kπ ∨ 2x = − 5π-+ 2k π ∨ 2x = π- + 2kπ / : 2 6 6 2 π-- 5π- π- x = − 12 + kπ ∨ x = − 12 + kπ ∨ x = 4 + kπ .

Teraz wystarczy wybrać te wartości 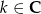k ∈ C , dla których 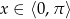x ∈ ⟨0,π ⟩ . Gdy to zrobimy, otrzymamy

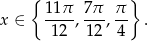
{ 11π 7π π} x ∈ ----,---, -- . 12 12 4

Odpowiedź: { } x ∈ π4-, 71π2, 111π2