/Szkoła średnia/Równania/Trygonometryczne/Stopnia 2

Zadanie nr 5826863

Wyznacz wszystkie rozwiązania równania 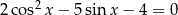2 2co s x − 5sin x− 4 = 0 należące do przedziału ⟨0,2π ⟩ .

Wersja PDF

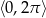Rozwiązanie

Korzystając z jedynki trygonometrycznej możemy dane równanie zapisać w postaci

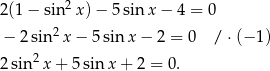
2 2(1 − sin x)− 5sin x− 4 = 0 − 2 sin 2x − 5sin x − 2 = 0 /⋅ (− 1) 2 sin 2x + 5 sin x + 2 = 0 .

Podstawiamy teraz 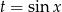t = sinx i mamy równanie

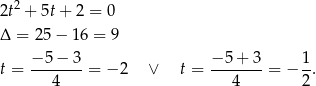
2t2 + 5t+ 2 = 0 Δ = 25 − 16 = 9 −-5-−-3 −-5-+-3 1- t = 4 = − 2 ∨ t = 4 = − 2.

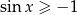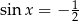Pierwsze rozwiązanie odrzucamy bo sinx ≥ − 1 i mamy sin x = − 12 .

PIC

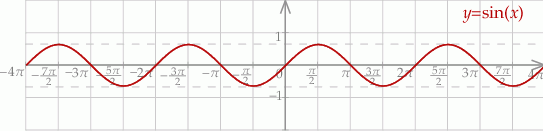
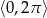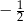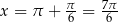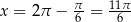W przedziale ⟨0,2π ⟩ sinus przyjmuje wartość − 12 w dwóch punktach, dla x = π + π-= 7π- 6 6 i x = 2π − π-= 11π- 6 6 .  
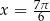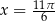Odpowiedź: 7π- x = 6 lub 11π- x = 6 .

Wersja PDF