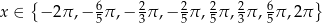Zadanie nr 7587638

Rozwiąż równanie 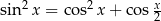2 2 x sin x = cos x + c os2 w przedziale ⟨− 2π ,2π⟩ .

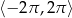Rozwiązanie

Sposób I

Skorzystamy ze wzorów

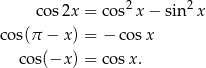
cos2x = cos2x − sin 2x cos(π − x ) = − cos x co s(−x ) = cos x.

Przekształcamy dane równanie.

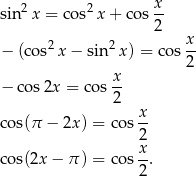
sin 2x = co s2x + cos x- 2 2 2 x- − (cos x− sin x) = co s2 x − cos 2x = cos -- 2 x cos(π − 2x ) = cos -- 2 cos(2x − π ) = cos x. 2

Szkicujemy teraz cosinusa.

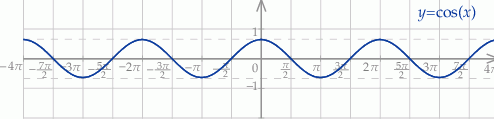
Z wykresu widać, że mamy dwie możliwości:

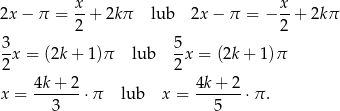
x- x- 2x− π = 2 + 2kπ lub 2x − π = − 2 + 2k π 3 5 -x = (2k+ 1)π lub -x = (2k + 1 )π 2 2 x = 4k-+-2-⋅π lub x = 4k+--2⋅ π. 3 5

W danym przedziale otrzymujemy stąd 8 rozwiązań:

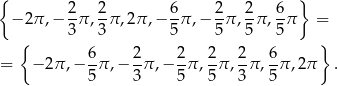
{ } −2 π,− 2-π, 2π ,2π,− 6-π,− 2π , 2π , 6π = 3 3 5 5 5 5 { 6 2 2 2 2 6 } = − 2π ,− --π,− --π,− --π, -π ,-π ,-π ,2π . 5 3 5 5 3 5

Sposób II

Tak samo jak poprzednio przekształcamy równanie do postaci

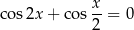
x- cos2x + cos2 = 0

Tym razem skorzystamy jednak ze wzoru na sumę cosinusów

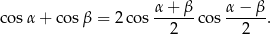
co sα + cos β = 2 cos α+--β-cos α-−-β-. 2 2

Mamy zatem

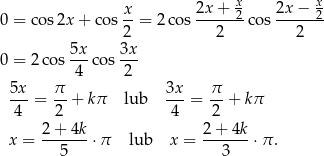
x 2x+ x 2x− x 0 = cos2x + cos-- = 2 cos -----2-cos -----2- 2 2 2 5x- 3x- 0 = 2co s 4 cos 2 5x π 3x π ---= --+ kπ lub --- = --+ kπ 4 2 4 2 x = 2-+-4k-⋅π lub x = 2+-4k-⋅ π. 5 3

Tak jak w poprzednim sposobie, otrzymujemy stąd

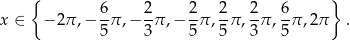
{ } x ∈ − 2π ,− 6π ,− 2π ,− 2π , 2π , 2-π, 6π ,2π . 5 3 5 5 3 5

Odpowiedź: { } x ∈ −2 π,− 6π ,− 2π ,− 2π , 2π , 2π , 6π ,2π 5 3 5 5 3 5