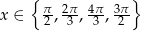Zadanie nr 7589013
Rozwiąż równanie 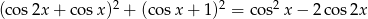 w przedziale
w przedziale 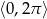 .
.
Rozwiązanie
Przekształcamy równanie
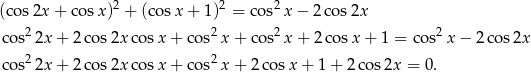
Ponieważ 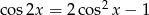 , to widać, że możemy w równaniu podstawić
, to widać, że możemy w równaniu podstawić 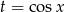 .
.
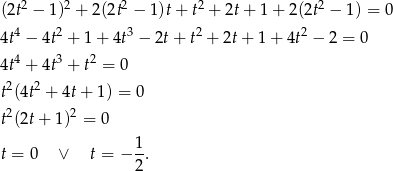
Zatem
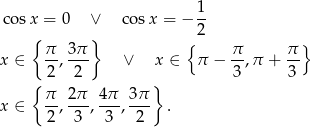
Odpowiedź: 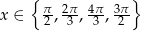
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 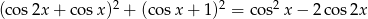 w przedziale
w przedziale 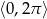 .
.
Przekształcamy równanie
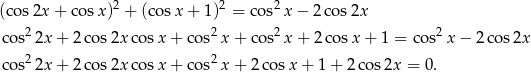
Ponieważ 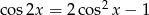 , to widać, że możemy w równaniu podstawić
, to widać, że możemy w równaniu podstawić 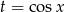 .
.
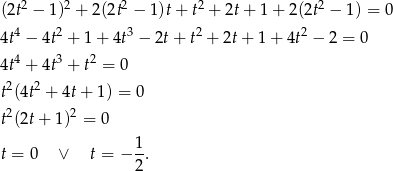
Zatem
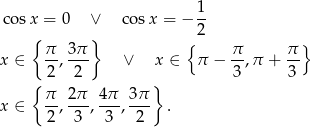
Odpowiedź: