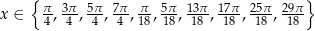Zadanie nr 8789585
Rozwiąż równanie 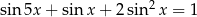 dla
dla 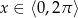 .
.
Rozwiązanie
Będziemy korzystać ze wzorów
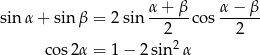
Przekształcamy dane równanie
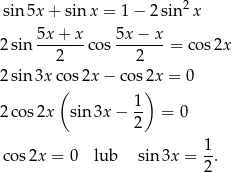
Szkicujemy sinusa i cosinusa.
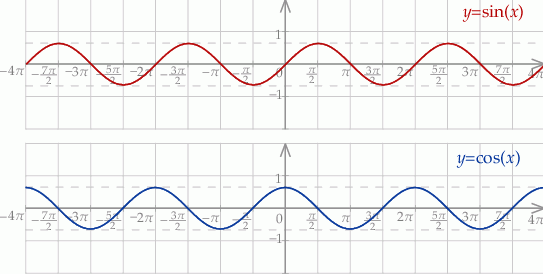
Z wykresów odczytujemy rozwiązania.
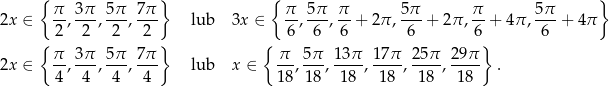
Odpowiedź: 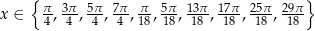
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 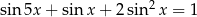 dla
dla 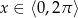 .
.
Będziemy korzystać ze wzorów
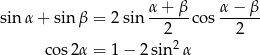
Przekształcamy dane równanie
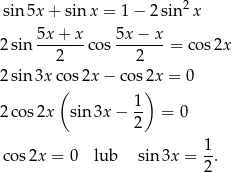
Szkicujemy sinusa i cosinusa.

Z wykresów odczytujemy rozwiązania.
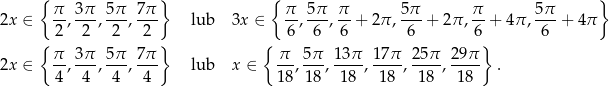
Odpowiedź: