Zadanie nr 9397556
Rozwiąż równanie ![[ ( π) ( π-)] 3 (sin x) ⋅ cos x− 6 + co s x + 6 = 2 cosx](https://img.zadania.info/zad/9397556/HzadT0x.gif) .
.
Rozwiązanie
Korzystamy ze wzoru na sumę cosinusów
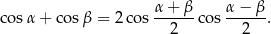
Przekształcamy dane równanie
![3 [ ( π ) ( π ) ] --cos x = (sin x)⋅ cos x− -- + cos x + -- 2 π- 6 π- 6π- π- 3-cos x = sin x⋅2 cos x-−-6-+-x-+--6-cos x−--6-−-x-−--6-= 2 2 2 3- ( π-) √ -- 2 cos x = sin x⋅2 cos xco s − 6 = 3sin xco sx (√ -- ) 0 = co sx 3 sin x − 3- . 2](https://img.zadania.info/zad/9397556/HzadR1x.gif)
Zatem 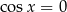 , czyli
, czyli 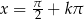 lub
lub 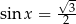 , czyli
, czyli 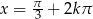 ,
, 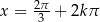 dla liczby całkowitej
dla liczby całkowitej 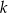 .
.
Odpowiedź: 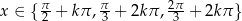 ,
, 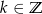
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie ![[ ( π) ( π-)] 3 (sin x) ⋅ cos x− 6 + co s x + 6 = 2 cosx](https://img.zadania.info/zad/9397556/HzadT0x.gif) .
.
Korzystamy ze wzoru na sumę cosinusów
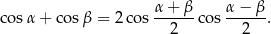
Przekształcamy dane równanie
![3 [ ( π ) ( π ) ] --cos x = (sin x)⋅ cos x− -- + cos x + -- 2 π- 6 π- 6π- π- 3-cos x = sin x⋅2 cos x-−-6-+-x-+--6-cos x−--6-−-x-−--6-= 2 2 2 3- ( π-) √ -- 2 cos x = sin x⋅2 cos xco s − 6 = 3sin xco sx (√ -- ) 0 = co sx 3 sin x − 3- . 2](https://img.zadania.info/zad/9397556/HzadR1x.gif)
Zatem 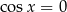 , czyli
, czyli 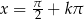 lub
lub 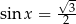 , czyli
, czyli 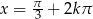 ,
, 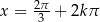 dla liczby całkowitej
dla liczby całkowitej 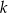 .
.

Odpowiedź: 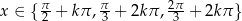 ,
,