/Szkoła średnia/Równania/Z wartością bezwględną/Wykładnicze

Zadanie nr 3467993

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 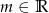m ∈ R równianie 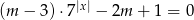|x| (m − 3) ⋅7 − 2m + 1 = 0 ma dwa różne rozwiązania?

Rozwiązanie

Zapiszmy równanie w postaci

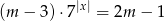
|x| (m − 3) ⋅7 = 2m − 1

Jeżeli 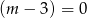(m − 3) = 0 , czyli 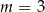m = 3 mamy sprzeczną równość 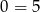0 = 5 . Możemy zatem założyć, że 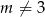m ⁄= 3 i wtedy możemy podzielić przez (m − 3) .

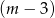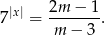
|x| 2m--−-1 7 = m − 3 .

Oczywiście aby równanie miało rozwiązanie prawa strona musi być dodatnia. Załóżmy, że tak jest (na razie nie sprawdzamy dla jakich x tak jest, jak za chwilę się okaże nie musimy tego robić). Jeżeli obie strony są dodatnie, możemy zlogarytmować stronami.

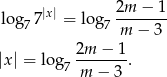
2m − 1 lo g77|x| = lo g7------- m − 3 2m-−--1 |x| = log7 m − 3 .

No i wszystko jasne, równanie będzie miało dwa rozwiązania jeżeli prawa strona jest dodatnia, czyli dla

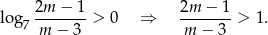
2m--−-1 2m--−-1 lo g7 m − 3 > 0 ⇒ m − 3 > 1.

Teraz widać dlaczego nie musieliśmy sprawdzać kiedy 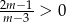2m−1- m− 3 > 0 , teraz sprawdzimy mocniejszą nierówność.

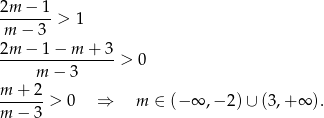
2m − 1 ------- > 1 m − 3 2m-−--1−--m-+-3-> 0 m − 3 m + 2 ------ > 0 ⇒ m ∈ (− ∞ ,− 2) ∪ (3,+ ∞ ). m − 3

 
Odpowiedź: m ∈ (− ∞ ,− 2)∪ (3,+ ∞ )

Wersja PDF