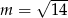/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 1925848

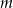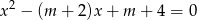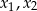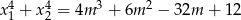Oblicz wszystkie wartości parametru m , dla których równanie x 2 − (m + 2)x + m + 4 = 0 ma dwa różne pierwiastki rzeczywiste x1,x 2 takie, że x41 + x42 = 4m 3 + 6m 2 − 32m + 12 .

Wersja PDF

Rozwiązanie

Sprawdźmy, kiedy równanie ma dwa różne pierwiastki

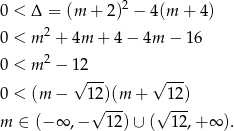
2 0 < Δ = (m + 2) − 4(m + 4) 0 < m 2 + 4m + 4− 4m − 16 2 0 < m − 12 0 < (m − √ 12)(m + √ 12) √ --- √ --- m ∈ (− ∞ ,− 1 2)∪ ( 12 ,+∞ ).

Korzystamy ze wzorów Viète’a.

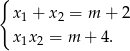
{ x1 + x2 = m + 2 x1x2 = m + 4.

Mamy zatem

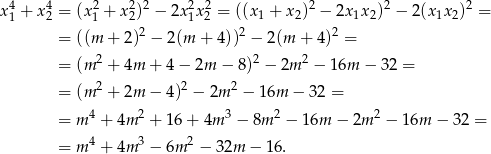
x 41 + x 42 = (x21 + x22)2 − 2x21x22 = ((x 1 + x 2)2 − 2x 1x2)2 − 2(x1x2)2 = 2 2 2 = ((m + 2 ) − 2(m + 4)) − 2(m + 4) = = (m 2 + 4m + 4 − 2m − 8)2 − 2m 2 − 1 6m − 32 = = (m 2 + 2m − 4)2 − 2m 2 − 16m − 32 = 4 2 3 2 2 = m + 4m + 16 + 4m − 8m − 16m − 2m − 16m − 32 = = m 4 + 4m 3 − 6m 2 − 32m − 16.

Musimy zatem rozwiązać równanie

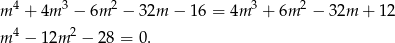
m 4 + 4m3 − 6m 2 − 32m − 16 = 4m 3 + 6m 2 − 32m + 12 4 2 m − 12m − 2 8 = 0.

Równanie jest dwukwadratowe, więc podstawiamy 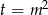t = m 2 .

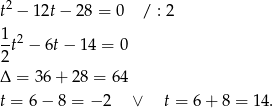
2 t − 12t− 28 = 0 / : 2 1 2 --t − 6t − 14 = 0 2 Δ = 36 + 28 = 64 t = 6 − 8 = − 2 ∨ t = 6+ 8 = 14.

Ujemne rozwiązanie odrzucamy (bo 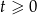t ≥ 0 ) i mamy 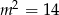m 2 = 14 , czyli 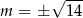√ --- m = ± 14 . Zauważmy, że dla każdej z tych wartości jest spełniony warunek Δ > 0 .  
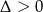Odpowiedź: 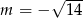√ --- m = − 14 lub √ --- m = 14

Wersja PDF