/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 2018969

Dla jakich wartości parametru 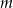m równanie 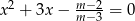2 m−-2 x + 3x − m− 3 = 0 ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru 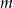m , dla których suma sześcianów pierwiastków tego równania jest równa -9.

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma pierwiastki

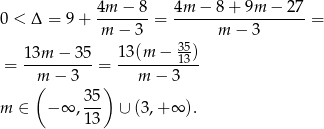
4m − 8 4m − 8 + 9m − 27 0 < Δ = 9+ ------- = ------------------= m − 3 m − 3 13m--−-35- 13(m--−-3153)- = m − 3 = m − 3 ( ) m ∈ − ∞ , 3-5 ∪ (3,+ ∞ ). 1 3

Skorzystamy teraz ze wzorów Viète’a

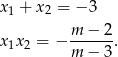
x1 + x2 = − 3 m − 2 x1x2 = − ------. m − 3

Liczymy

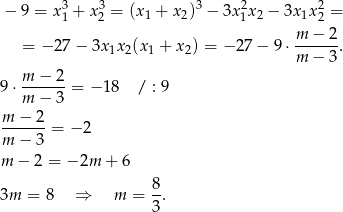
− 9 = x3+ x3 = (x + x )3 − 3x2x − 3x x2= 1 2 1 2 1 2 1 2 = − 27 − 3x x (x + x ) = − 27− 9⋅ m-−-2-. 1 2 1 2 m − 3 m − 2 9⋅ ------= − 18 / : 9 m − 3 m-−-2-= − 2 m − 3 m − 2 = − 2m + 6 3m = 8 ⇒ m = 8-. 3

 
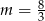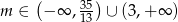Odpowiedź: 8 m = 3 . Pierwiastki dla ( ) m ∈ − ∞ , 3153 ∪ (3,+ ∞ ) .

Wersja PDF