/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 2148088

Dla jakich wartości parametru 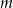m równanie 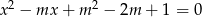2 2 x − mx + m − 2m + 1 = 0 ma dwa różne pierwiastki rzeczywiste, których suma jest o jeden większa od ich iloczynu?

Wersja PDF

Rozwiązanie

Zadanie będziemy chcieli rozwiązać używając wzorów Viète’a.

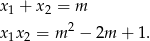
x + x = m 1 2 x1x2 = m 2 − 2m + 1.

Aby to zrobić powinniśmy w zasadzie sprawdzić, kiedy równanie ma w ogóle pierwiastki – jednak zamiast to robić, na koniec sprawdzimy poprawność otrzymanych rozwiązań.

Musimy rozwiązać równanie

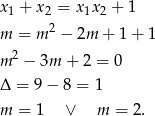
x1 + x2 = x1x2 + 1 m = m 2 − 2m + 1+ 1 m 2 − 3m + 2 = 0 Δ = 9 − 8 = 1 m = 1 ∨ m = 2.

Łątwo sprawdzić, że dla 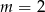m = 2 jest jeden pierwiastek podwójny, a dla 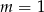m = 1 są dwa różne.  
Odpowiedź: m = 1

Wersja PDF